Als Jugendliche und junge Erwachsene gab ich Nachhilfe in Mathematik. Ich unterrichtete alle Klassenstufen bis zum Abitur. Dabei fiel mir auf, dass viele Jugendliche, die zu mir kamen, Probleme mit der Bruchrechnung hatten. Schlimmer noch: Sie hatten häufig überhaupt gar keine Vorstellung davon, wie viel ein Viertel oder ein Achtel ist. Ich begann also ganz von vorn und gab ihnen eine Einführung in die Bruchrechnung.
Hierzu benutzte ich Gegenstände, welche die Jugendlichen aus ihrem Alltag kannten. Zum Beispiel einen Apfel. Ich zerschnitt ihn in zwei Hälften. Ein halber Apfel oder mathematisch ausgedrückt 1/2 Apfel. Teilte ich die beiden Hälften weiter, so entstanden vier Teile. Jedes dieser Teile nennen wir ein Viertel (in der mathematischen Schreibweise 1/4).

Es ist also im Grunde ganz einfach: Wird ein Gegenstand in mehrere gleichgroße Stücke geteilt, so können wir jedes einzelne dieser (Bruch)Stücke mathematisch beschreiben, indem wir oberhalb des Bruchstrichs eine eins schreiben und unterhalb des Bruchstrichs die Gesamtanzahl der Stücke.
Den Bruch an sich verstehen
Bevor ich den Jugendlichen also beibrachte mit Brüchen zu rechnen, sorgte ich erst einmal dafür, dass sie ein Verständnis davon entwickelten, was eine Bruchzahl überhaupt ist. Dies funktioniert nicht nur mit einem Apfel, sondern auch mit einer Tafel Schokolade, einer Pizza, einem Kuchen oder einem beliebigen anderen teilbaren Gegenstand. Wie immer empfiehlt es sich, die Vorlieben des Lernenden bei der Auswahl zu berücksichtigen.
Darüber hinaus vergewisserte ich mich, dass die grundlegenden Begriffe verstanden wurden. So fragte ich zum Beispiel ab, was ein Bruchstrich ist oder überprüfte, ob den Jugendlichen klar war, dass die Zahl oberhalb des Bruchstriches Zähler und die Zahl unterhalb des Bruchstriches Nenner genannt wird. Denn mit einem einheitlichen Vokabular lässt es sich gleich viel besser miteinander kommunizieren.
Bisher haben wir also Brüche kennen gelernt, deren Zähler eins beträgt. Zum Beispiel 1/6 Pizza. Doch wer wird schon von einem Sechstel Pizza satt? Wenn meine Pizza in sechs Teile unterteilt wäre, hätte ich gerne mindestens zwei Stücke davon. Ich hätte also gerne zwei Sechstel. Mathematisch betrachtet würde das dann so aussehen: 2/6.
„Ernsthaft? Du wirst von zwei Stückchen Pizza satt?“, fragten mich die Jugendlichen in der Regel. „Nee, natürlich nicht!“, war meine Antwort. „Kannst du mir mal 3/6 aufmalen? … Und 4/6? … Wie sehen 5/6 aus? Ah, ich denke, jetzt bin ich satt geworden.“
Brüche umformen
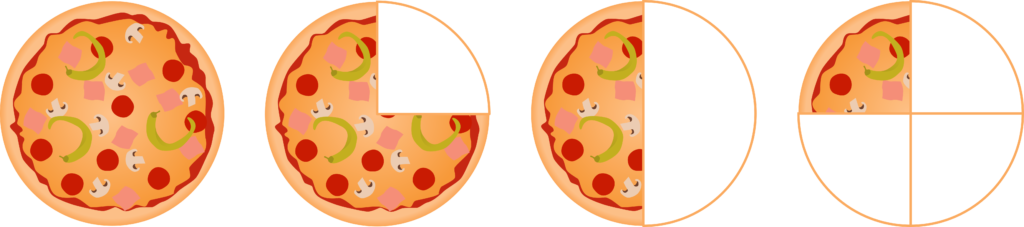
„Also ich würde mehr schaffen!“, meinten die Jugendlichen nicht selten. Okay, schauen wir also was passiert, wenn man noch ein weiteres Stück Pizza isst. Zur Veranschaulichung eignen sich sowohl eine echte Pizza, als auch ein in Stücke geschnittener Kreis oder eine einfache Handzeichnung. Stellen wir uns also vor, jemand möchte 6/6 Pizza essen. Schneiden wir die Pizza also in sechs Teile und nehmen uns sechs Teile. Wir stellen fest, dass wir nun die ganze Pizza haben. 6/6 ist also das Gleiche wie 1.
Dieses Spielchen können wir nun auch mit anderen Zahlen machen. Schneiden wir die Pizza in vier Teile und nehmen uns alle vier Teile, so haben wir eine ganze Pizza. 4/4 ist also gleich 1.
Wir merken uns also: Sind Zähler und Nenner identisch, so ergibt dies 1.
Brüche kürzen
Manch einem gewitzten Jugendlichen ist noch etwas aufgefallen: Drei Sechstel Pizza sehen genauso aus wie eine halbe Pizza. „Ist das Zufall?“ „Nein!“
3/6 ist das Gleiche wie 1/2. „Findet ihr weitere Brüche, die gleich 1/2 sind?“, fragte ich die Jugendlichen. Zum Lösen dieser Aufgabe ist Legematerial sehr hilfreich. Man kann hierzu ganz einfach auf Pappkreise zurück greifen, welche in unterschiedlich viele jeweils gleich große Teile zerschnitten wurden. Mit Hilfe dieses Materials wird schnell klar, dass auch 2/4 und 4/8 gleich 1/2 sind.
Schauen wir uns diese Zahlen also einmal genauer an. 2/4, 3/6 und 4/8 sind gleich 1/2. Fällt uns etwas auf? Bei all diesen Brüchen ist der Nenner doppelt so groß wie der Zähler.
Da Brüche mit großen Zahlen häufig unübersichtlich werden, kann man diese vereinfachen. Wir nennen dies „kürzen“. Das Kürzen erlaubt es uns aus komplizierten Zahlengebilden wie 473/946 einfache und begreifbare Zahlen zu machen. In diesem Falle kommen wir durch Kürzen auf 1/2.
Wie funktioniert dieses Kürzen genau? Im Grunde ist es ganz einfach: Wir suchen nach einem gemeinsamen Teiler von Zähler und Nenner. Haben wir einen gefunden, so teilen wir Zähler und Nenner durch den gefundenen Teiler. Fertig.
Ein Beispiel: Wollen wir den Bruch 4/8 kürzen, so fällt uns vielleicht auf, dass man Zähler und auch Nenner durch zwei teilen kann. Auf diese Weise erhalten wir 2/4. Das sieht schon einfacher aus, aber es geht noch besser, denn zwei und vier lassen sich wiederum durch zwei teilen. Wir erhalten 1/2. Diesen Bruch können wir nicht weiter kürzen.
Brüche erweitern
Dieses Prinzip funktioniert auch anders herum. Das bedeutet, dass wir Zähler und Nenner mit der gleichen Zahl multiplizieren dürfen um ein gleichwertiges Ergebnis zu erhalten. Wir sprechen hier vom „erweitern“. Nehmen wir uns als Beispiel den Bruch 1/3. Wenn wir diesen so erweitern wollen, dass wir als Nenner 15 erhalten, so dürfen wir Zähler und Nenner mit fünf multiplizieren und erhalten 5/15.
Das Erweitern benötigen wir später für verschiedene Rechenoperationen mit Brüchen. An dieser Stelle ist es zunächst nur hilfreich zu wissen, dass das Prinzip des Kürzens grundsätzlich auch anders herum möglich und erlaubt ist.
Brüche verstanden?
Euch raucht der Kopf? Kein Wunder. Das waren viele Informationen auf einmal. Kinder und Jugendliche sollten dies in mehreren kleinen Portionen erlernen. Natürlich sollten die Inhalte nicht nur verstanden, sondern auch angewandt werden. Hierzu gibt es vielzählige Übungen im Mathebuch oder online.
Die gute Nachricht ist, dass meiner Erfahrung nach auch schon Grundschüler mit der Materie umgehen können, wenn man sie ihnen Schritt für Schritt näher bringt. Wichtig ist, dass jeder einzelne Schritt verstanden und begriffen wird. Darum ist es mir wichtig nicht bloß mit irgendwelchen Zahlen und Formeln um mich zu schmeißen, sondern den Kindern konkrete Gegenstände an die Hand zu geben. So haben sie die Chance, sich spielerisch anzunähern.

Bereit für den nächsten Schritt? Nun folgen die ersten echten Rechenoperationen.
Einführung in die Bruchrechnung
Halten wir gleich zu Anfang fest: Die bisher bekannten Rechenoperationen Addition, Subtraktion, Multiplikation und Division sind auch mit Brüchen möglich. Wie das genau funktioniert, sehen wir im Folgenden:
Brüche addieren
„Stell dir vor, du hast Geburtstag. Deine Mama hat dir eine Torte gebacken. Mit saftigem Boden, viel Schokolade und leckerer Sahne! Sie schneidet den Kuchen in zwölf Stücke. Wie viel vom ganzen Kuchen hast du gegessen, wenn das erste Stück in deinem Magen gelandet ist?“, fragte ich meine Jugendlichen. Dies ist eine einfache Wiederholung des bereits Gelernten. „Ein Zwölftel natürlich!“, lautete ihre Antwort. „Okay, stell dir nun vor, du isst ein zweites Stück.“ „Dann sind es 2/12.“ „Ganz genau.“
Damit haben wir bereits die erste kleine Additionsaufgabe bewältigt. 1/12 + 1/12 = 2/12
Gleicher Nenner
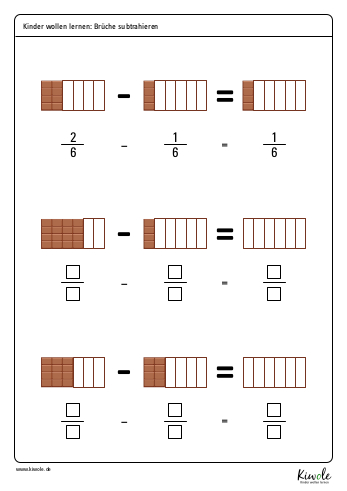
Natürlich lassen sich Aufgaben wie diese auch wieder mit Pappkreisen nachlegen, was schließlich zu der Erkenntnis führt: Bei der Addition zweier Brüche mit identischem Nenner werden die Zähler miteinander addiert, während der Nenner gleich bleibt.
Noch einmal anschaulich: In unserem Beispiel 1/12 + 1/12 addieren wir die Zähler (1+1=2) und behalten den Nenner bei. So erhalten wir die Lösung 2/12.
Ungleicher Nenner
Etwas schwieriger wird es, wenn die Nenner nicht identisch sind. Stellen wir uns dies also zunächst wieder bildlich vor:
„Deine Tante bringt dir eine zweite Geburtstagstorte mit. Die Torte deiner Mutter wurde in zwölf Teile geschnitten und nachdem ihr euch alle satt gegessen habt, bleiben noch drei Stücke übrig. Ihr habt also noch 3/12 der ersten Torte. Die Torte deiner Tante wurde in acht Stücke unterteilt. Davon sind zwei Stücke übrig geblieben. Es bleiben dir also 2/8 der zweiten Torte. Wie viel Torte habt ihr nun insgesamt noch übrig?“
Wenn wir diese Aufgabe legen, sehen wir schnell, dass noch eine halbe Torte übrig ist. Doch wie können wir das rechnerisch lösen?
Das Problem besteht darin, dass wir die Zähler nicht einfach miteinander addieren können, wenn die Nenner unterschiedlich sind. Wir müssen also dafür sorgen, dass die Nenner gleich werden. Kein Problem! Immerhin dürfen wir die Brüche ja kürzen oder erweitern. Und genau das tun wir nun so lange, bis wir identische Nenner erhalten.
Im oberen Beispiel 3/12 + 2/8 können wir beide Brüche kürzen und erhalten so die einfache Aufgabe 1/4 + 1/4 = 2/4 Auch das Ergebnis kann gekürzt werden, so dass wir zu unserer gelegten Lösung von 1/2 kommen.
„Stellen wir uns vor, dass von der ersten Torte sieben Stücke übrige geblieben sind und von der zweiten Torte drei Stücke. Wie viel Torte bleibt uns insgesamt?“ In diesem Falle stehen wir vor der Aufgabe 7/12 + 3/8. Kürzen ist unmöglich. Daher erweitern wir beide Brüche um einen gemeinsamen Nenner zu erhalten. Wir suchen also das kleinste gemeinsame Vielfache von zwölf und acht. (Im Grunde suchen wir einfach irgendein gemeinsames Vielfaches von zwölf und acht, aber um die Sache nicht unnötig kompliziert zu machen, ist es in der Regel am einfachsten das kleinste gemeinsame Vielfache zu suchen.) Dies ist 24. Wir erweitern also beide Brüche so, dass ihr Nenner 24 wird und erhalten 14/24 + 9/24. Diese Aufgabe können wir nach den oben genannten Regeln lösen. Das Ergebnis lautet 23/24. Es bleibt also beinahe eine ganze Torte.
Brüche subtrahieren
Ist die Addition von Brüchen verstanden und geübt, so ist die Subtraktion ein Kinderspiel.
Gleicher Nenner
„Es ist ein heißer Sommertag und im Kühlschrank liegt noch eine 3/4 Wassermelone. Du isst 1/4 davon. Wie viel bleibt übrig?“
Analog zu unserer Rechenweise in der Addition dürfen wir auch bei der Subtraktion den Nenner unberührt lassen, wenn dieser identisch ist und lediglich mit dem Zähler rechnen. Im oberen Beispiel müssten wir also 3-1=2 rechnen, den Nenner beibehalten und würden als Ergebnis 2/4 oder gekürzt 1/2 erhalten.
Unterschiedlicher Nenner
„Du entscheidet sich anders und isst von deiner 3/4 Melone 3/8. Wie viel bleibt übrig?“
In diesem Falle müssen wir dafür sorgen, dass die Nenner durch kürzen oder erweitern aneinander angeglichen werden. Dies ist simpel und wir erhalten die Aufgabe 6/8 – 3/8 = 3/8.
Einen Sonderfall stellt die Zahl 1 dar. „Angenommen du hast eine ganze Tafel Schokolade und isst 5/6 davon auf. Wie viel Schokolade bleibt dir für später?“ Die dazugehörige Aufgabe lautet 1 – 5/6
Wie können wir bei dieser Aufgabe gleiche Nenner erhalten? Ganz einfach, erinnern wir uns daran, dass 6/6 Pizza gleich 1 war und 4/4 Pizza ebenfalls gleich 1, so liegt der Gedanke nahe, dass wir unsere 1 in 6/6 umwandeln können. Die Aufgabe lautet nun 6/6 – 5/6 = 1/6

Einführung in die Bruchrechnung geglückt?
Ich hoffe, meine kleine Einführung in die Bruchrechnung konnte euch helfen. Lernplakate findet ihr in meinem Shop. Anschauungs- und Lernmaterial zum Thema habe ich euch auf eduki hinterlegt. Zum Beispiel dieses:
- Einführung in die Bruchrechnung mit Pizza-Bildkarten
- Brüche und Bruchdarstellung mit Pizza und Schokolade
- Brüche vergleichen mit Waffeln und Pizza
- Kinderrätsel zur Hinführung an die Bruchrechnung (den dazugehörigen Blogartikel findet ihr hier)
- Addition von Brüchen, hier eine kleine Kostprobe:
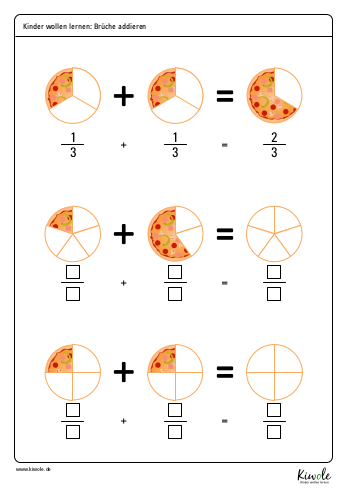
- Unechte Brüche addieren
- Subtraktion von Brüchen, auch hierzu eine kleine Kostprobe: