Heute gebe ich euch eine kurze Einführung zum Satz des Thales. Voraussetzung für das Verständnis ist die Kenntnis des rechten Winkels beziehungsweise des rechtwinkligen Dreiecks. Lest euch gegebenenfalls noch einmal meine Blogartikel „Faszination Winkel – Der rechte Winkel“ sowie „Dreiecksarten – Dreiecke auf clevere Art unterscheiden lernen“ zur Erinnerung durch.
Was besagt der Satz des Thales?
Konstruiert man ein Dreieck aus den beiden Endpunkten eines Halbkreises und einem weiteren Punkt, welcher auf dem Halbkreis liegt, so erhält man immer ein rechtwinkliges Dreieck!
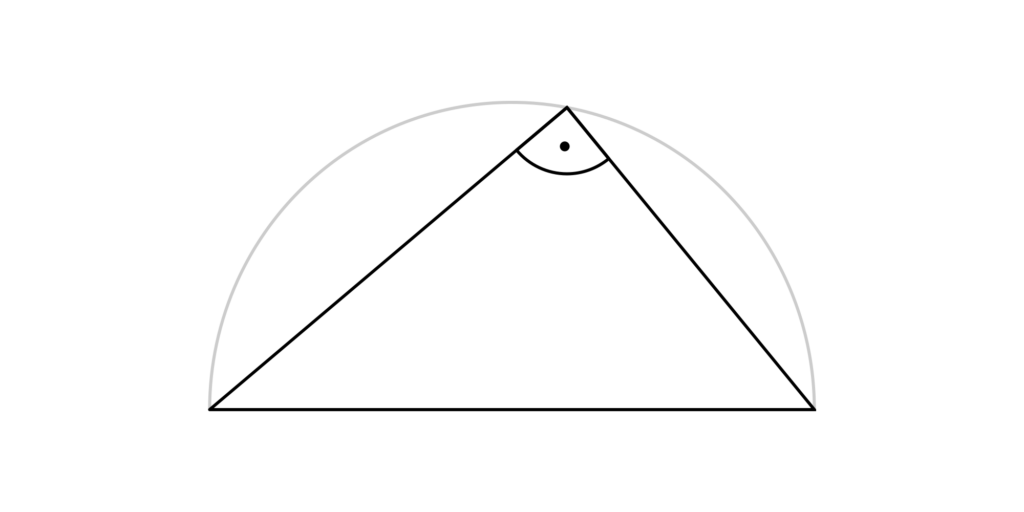
Der erste Beweis dieses Satzes wird dem antiken griechischen Mathematiker Thales von Milet zugeschrieben. Daher sprechen wir heute vom „Satz des Thales“. Den Halbkreis nennen wir entsprechend Thaleskreis.
Probiere es einfach einmal aus: Zeichne einen Halbkreis. Benenne die Endpunkte A und B. Bestimme einen Punkt C, der auf dem Halbkreis liegt. Verbinde die Punkte A, B und C zu einem Dreieck. Miss den Winkel γ. Egal wo du deinen Punkt C auf dem Halbkreis platziert hast, γ ist immer genau 90° groß.
Diese Erkenntnis kann bereits bei relativ jungen Schülerinnen und Schülern für Faszination sorgen. Sobald Dreiecke und der rechte Winkel bekannt sind, kann der Satz des Thales daher (meine Meinung nach) als Fordermaterial zum Einsatz kommen.
Wie der Thaleskreis im schulischen Kontext eingeführt werden kann
Ein befreundeter Lehrer setzte den Thaleskreis spielerisch in einer Vertretungsstunde ein. Er zeichnete mit Kreide einen großen Halbkreis auf den Schulhof und beschriftete die Endpunkte mit A und B. Er forderte die Schülerinnen und Schüler auf, sich auf den Halbkreis zu stellen und jeweils eine Fußspitze zum Punkt A und eine zum Punkt B zeigen zu lassen. Wo muss man stehen, um den größten Winkel zwischen seinen beiden Füßen zu erhalten? Die Schülerinnen und Schüler probierten es aus, bis sie schließlich zu der Erkenntnis kamen, dass der Winkel überall gleich groß ist. (Welch eine tolle Vertretungsstunde! Ich wünschte, alle Lehrer wären so engagiert!)
Anwendungsbeispiele
Der Satz des Thales kann dir bei der Berechnung der Winkel im Dreieck nützlich sein. Wir wissen, dass der rechte Winkel exakt 90° groß ist. Auch ist uns bekannt, dass die Winkelsumme im Dreieck 180° beträgt. Ist nun die Größe eines weiteren Winkels bekannt, kann die Größe des letzten Winkels rechnerisch ermittelt werden. Probiere es mit Hilfe des folgenden Arbeitsblattes aus:
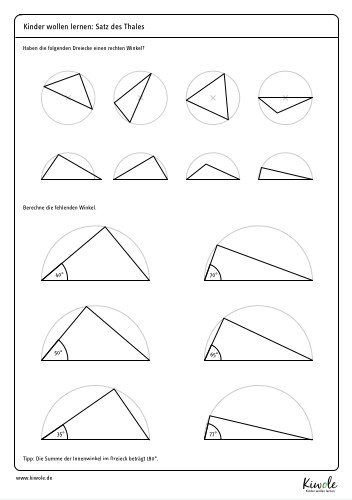
Darüber hinaus hilft der Satz des Thales bei der Konstruktion von Dreiecken.
Weitere Arbeitsblätter zum Thema findest du auf Eduki in meinen Materialien:
- Der Satz des Thales – Einführung
- Satz des Thales – Winkel berechnen und vermischte Aufgaben
- Der Satz des Thales – Dreiecke konstruieren
Alle drei Materialien sind auch gemeinsam als Materialpaket erhältlich.


Hallo könnten sie oder er bitte die Lösungen zum arbeitsblatt von Dem thales kreis mir per email schicken da ich eine präsentation halten muss und ich dafür lösungen brauche wäre nett danke
Hallo Lara,
gerne helfe ich dir bei Verständnisproblemen weiter. Wo genau hast du etwas nicht verstanden?