Ihr liebt meine zahlreichen Artikel zum Thema Achsensymmetrie ebenso wie meinen Artikel zum Koordinatensystem. Warum also nicht beides miteinander verbinden? Heute werfen wir also einen Blick auf die Achsensymmetrie im Koordinatensystem.
Wiederholung Symmetrie und Koordinatensystem
Falls ihr euch im Bereich der Achsensymmetrie noch unsicher fühlt, empfehle ich euch die folgenden Artikel:
- Achsensymmetrie durch spiegeln begreifen
- Spiegelachsen finden und einzeichnen
- Symmetrische Figuren frei Hand zu Ende zeichnen
- Spiegelbilder im Gitternetz
- Symmetrische Figuren vervollständigen
Zur Wiederholung des Themas Koordinatensysteme eignet sich der umfangreiche Artikel „Einführung in die Koordinatensysteme„.
Symmetrische Figuren im Koordinatensystem
Auch im Koordinatensystem werden die einzelnen Punkte an einer Achse gespiegelt. Als Achse dient entweder die x-Achse, die y-Achse oder eine vorgegebene Gerade. Um die Spiegelachse als solche hervorzuheben, empfehle ich sie stets rot einzuzeichnen. Statt Spiegelachse darfst du auch Symmetrieachse sagen.
Die gespiegelten Punkte nennen wir Bildpunkte. Zu jedem Punkt gibt es genau einen Bildpunkt. Wir kennzeichnen die Bildpunkte mit einem kleinen Strich. So ergibt sich zum Punkt A der Bildpunkt A‘, zum Punkt B gehört der Bildpunkt B‘ und so weiter. Ein Sonderfall tritt auf, wenn ein Punkt genau auf der Spiegelachse liegt. In diesem Fall ist der Bildpunkt gleich dem Originalpunkt. Liegt der Punkt C beispielsweise auf der Symmetrieachse, so gilt C=C‘.
Beachte, dass der Abstand von Punkt und Bildpunkt zur Spiegelachse stets gleich groß ist. Liegt die Spiegelachse waagerecht oder senkrecht, so kann es helfen die Kästchen zwischen Punkt und Spiegelachse zu zählen. Auch ein Geodreieck kann dir helfen: Indem du die Nulllinie des Geodreiecks genau auf die Symmetrieachse legst, ist sichergestellt, dass der Winkel stimmt und es fällt dir deutlich leichter den Abstand in beide Richtungen zu bestimmen. Die Methode mit dem Geodreieck funktioniert übrigens auch dann, wenn die Spiegelachse nicht senkrecht oder waagerecht liegt. Probiere es einfach mal aus!
Arbeitsblätter
Nach der Theorie folgt die Praxis. Hast du alles zum Thema „Achsensymmetrie im Koordinatensystem“ verstanden? Das folgende Arbeitsblatt hilft dir dein Wissen zu testen:
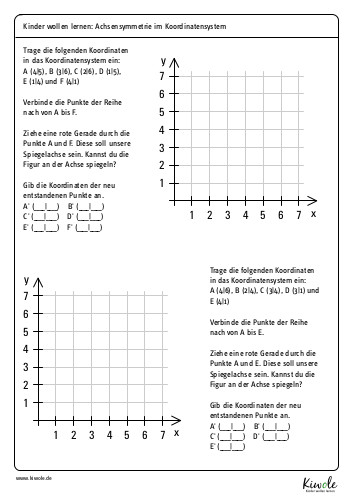
Weitere Arbeitsblätter dieser Art findest du auf eduki. Ich wünsche dir viel Spaß damit!