Die Drehsymmetrie (auch Rotationssymmetrie genannt) ist eine Form der Symmetrie, die uns im Alltag weniger häufig begegnet und uns daher fremder ist als die Achsensymmetrie. Wir können sie zum Beispiel beim Recycling-Zeichen, in Mandalas oder in symbolhaften Darstellungen von Sternen und Blumen beobachten.
Drehsymmetrie – was ist das überhaupt?
Eine Figur ist drehsymmetrisch, wenn man sie drehen kann und sie sich dabei auf sich selbst abbildet. Nehmen wir ein Beispiel:
Stellen wir uns ein Quadrat vor. Dreht man es um 90°, so erhält man die gleiche Figur wie zuvor. Das Quadrat ist demnach drehsymmetrisch.
Dies funktioniert aber nicht nur mit einem Winkel von 90°, sondern zum Beispiel auch mit einem Winkel von 180°. Ein gutes Beispiel hierfür ist ein Rechteck. Dreht man dieses um 180°, so erhält man exakt die gleiche Figur wie zuvor.
Auch Seesterne sind (annähernd) drehsymmetrisch. Dreht man sie um 72°, so erhält man (in etwa) das gleiche Bild wie zuvor.
Fallen euch weitere drehsymmetrische Figuren ein?
Symmetrie zum Anfassen
Erinnert ihr euch noch an die Spiegelachse bei der Achsensymmetrie? Sie ist stets rot dargestellt. In der Drehsymmetrie hingegen gibt es statt der Spiegelachse nur einen Spiegelpunkt. Diesen habe ich euch auf dem folgenden Arbeitsblatt ebenfalls rot dargestellt:
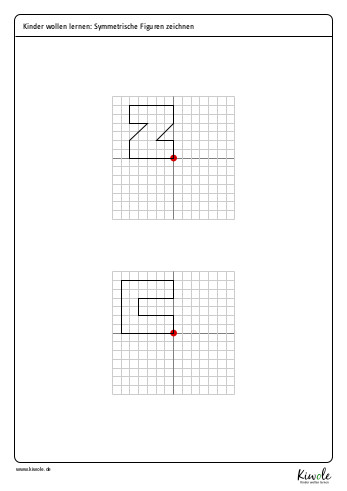
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Die Aufgabe deines Kindes besteht nun darin, die Figur aus dem ersten Quadrat um den Drehpunkt zu drehen und in die anderen drei Quadrate zu übertragen. Um dies begreifbarer zu machen, habe ich meiner Tochter die folgende kleine Hilfestellung gebastelt:

Um diese nachzubauen, benötigt ihr lediglich eine Schere, etwas Pappe für mehr Stabilität, eine Musterbeutelklammer und das folgende Arbeitsblatt:
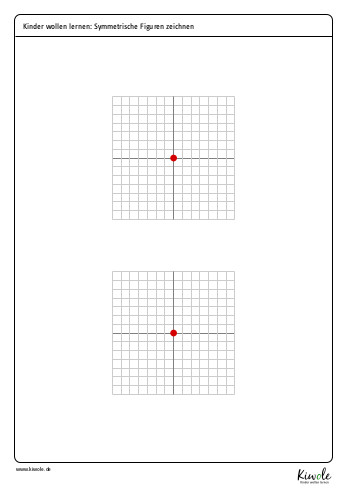
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Weitere Arbeitsblätter findet ihr wie immer auf eduki (hier und hier). Ich wünsche euch viel Spaß beim Entdecken der Drehsymmetrie!
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)