Das Kommutativgesetz besagt, dass du die Summanden bei einer Addition vertauschen darfst. Dies ändert nichts am Ergebnis!
Nehmen wir ein einfaches Beispiel:
2+4=6
4+2=6
Wir können diesen Sachverhalt auch mit Hilfe einer Waage veranschaulichen:
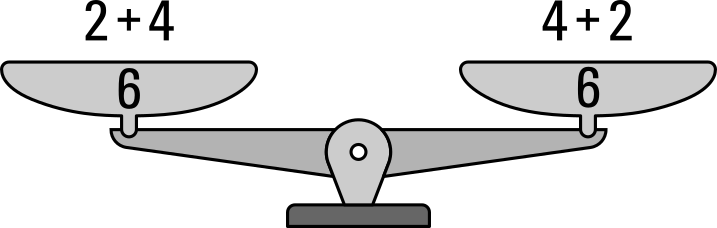
Doch wofür brauchen wir das Kommutativgesetz überhaupt? Manchmal ist es hilfreich die Tauschaufgabe zu bilden, da die Tauschaufgabe im Kopf leichter lösbar ist. Auch hierzu ein kleines Beispiel: Du sollst die Aufgabe 6+13 lösen. Den meisten Menschen fällt es stattdessen leichter das Ergebnis von 13+6 zu bestimmen.
Im Folgenden einige Übungsaufgaben. Welche Aufgabe ist für dich einfacher zu berechnen?
5+14 oder 14+5
7+9 oder 9+7
3+55 oder 55+3
13+17 oder 17+13
Das Kommutativgesetz gilt ebenso bei der Multiplikation! Du darfst die Faktoren miteinander vertauschen. Es wird sich nichts am Ergebnis verändern.
Schau dir das folgende Beispiel an:
2×4=8
4×2=8
Auch hierzu eine kleine Veranschaulichung mit Hilfe unserer Waage:
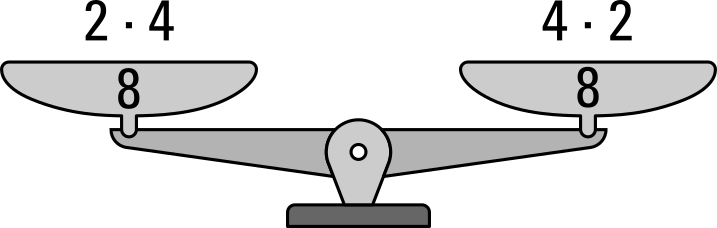
Entscheide bei den folgenden Übungsaufgaben, welche Aufgabe für dich leichter zu rechnen ist:
8×2 oder 2×8
7×5 oder 5×7
9×11 oder 11×9
17×2 oder 2×17
Das Kommutativgesetzt gilt jedoch NICHT bei der Subtraktion und auch NICHT bei der Division! Die beiden Waagen zeigen es sehr anschaulich.
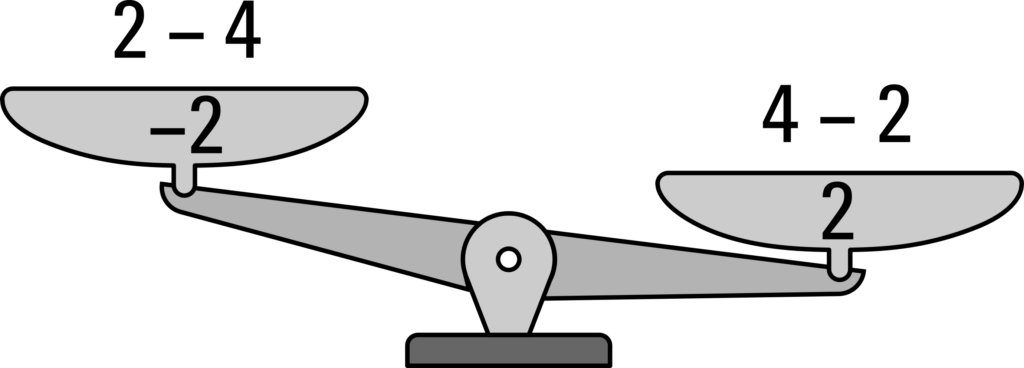
Ganz besonders hilfreich wird das Kommutativgesetz bei größeren und längeren Aufgaben. Es erlaubt uns, auch schwierig anmutende Aufgaben wie die Folgenden im Kopf zu lösen:
55+13+45+87=
4+64+96+36=
4x7x5x5=
5x13x2=
Tauschaufgaben kannst du übrigens auch bei negativen Zahlen und bei Brüchen bilden. Sie können dir auch hier großartig weiterhelfen!
Übungsaufgaben in unterschiedlichen Schwierigkeitsstufen findet ihr in meinem Eduki-Material „Kommutativgesetz – Einführung in die Tauschaufgaben„. Es kann bereits von Grundschülern erarbeitet werden. Ich wünsche euch viel Spaß damit!
