In der Schule taucht das Thema „Flächeninhalt“ in unterschiedlichen Klassenstufen immer wieder auf. Die Schülerinnen und Schüler berechnen den Flächeninhalt von Dreiecken, Trapezen, Kreisen und vielen anderen geometrischen Figuren. Doch zu allererst berechnen sie den Flächeninhalt von Rechtecken und Quadraten. An dieser Stelle sollten die Schülerinnen und Schüler verstehen, was der Begriff „Flächeninhalt“ bedeutet. Außerdem wird zum ersten Mal eine Formel hergeleitet und das Einsetzen von Werten in eine Formel geübt.
Formeln für den Flächeninhalt von Rechteck und Quadrat
Die Formel für den Flächeninhalt eines Rechtecks lautet: A = a ⋅ b
Das kleine a steht hierbei für die eine Seite des Rechtecks und das kleine b für die andere Seite des Rechtecks. Ist dieser Zusammenhang verstanden, lässt sich hieraus leicht die Formel für den Flächeninhalt eines Quadrats ableiten: A = a ⋅ a oder vereinfacht ausgedrückt A = a², denn bei einem Quadrat sind bekanntlich alle Seiten gleich lang.
Ein anschaulicher Einstieg ins Thema „Flächeninhalt vom Rechteck“
Um deinem Kind den Einstig in dieses so wichtige, grundlegende Thema zu vereinfachen, empfehle ich anschauliche Beispiele aus dem Alltag des Kindes zu finden. Hierzu eignet sich vor allem die Renovierung eines Raumes (idealerweise natürlich die Renovierung des Kinderzimmers). Nehmen wir an, ein neuer Fußbodenbelag soll verlegt werden und die Wände sollen neu gestrichen werden.

Zunächst einmal kann das Kind mit Hilfe eines Zollstocks die Wände vermessen und Skizzen mit den ermittelten Daten erstellen. Wenn man im Anschluss daran gemeinsam in einen Baumarkt fährt um mögliche Materialien zu inspizieren, wird schnell die Frage aufkommen: „Wie viel Farbe benötigen wir denn eigentlich?“
Auf jedem Farbeimer ist vermerkt für wie viele Quadratmeter die Farbe ausreicht. Nun heißt es rechnen. Wie groß ist unsere Wand? Wie viele Quadratmeter sind das? Und was ist überhaupt ein Quadratmeter?
Ein Quadratmeter
Um ein Gefühl dafür zu bekommen wie groß ein Quadratmeter ist, empfehle ich zu Hause einfach mal einen Quadratmeter auszuschneiden. Dafür nehmt ihr ein großes Stück Pappe oder Papier und schneidet es so zurecht, dass ein Quadrat mit einer Seitenlänge von einem Meter entsteht. Vielleicht müsst ihr auch mehrere Stücke Papier zusammenkleben. Beziehe dein Kind mit ein! Es wird sicher eine gute Lösung finden. In die Mitte des Papiers oder der Pappe kann nun vermerkt werden: 1 m² (ein Quadratmeter)
Ein Quadratmeter ist ganz schön groß. Auf dieser Fläche können ziemlich viele Spielzeugautos parken. Man kann ein wunderbar großes Bild darauf malen. Oder die Fläche auf andere Art und Weise bespielen. In diesem ersten Schritt geht es zunächst einmal darum ein Gespür für die Größe der Fläche zu entwickeln. Es ist auch möglich einen Quadratmeter mit Straßenkreide auf den Gehweg zu zeichnen und die Fläche durch hüpfen, turnen oder das Abspritzen mit einer Wasserpistole zu begreifen.
Quadratmeter, Quadratdezimeter, Quadratzentimeter
Im Folgenden kann die gleiche Übung mit einem Quadratdezimeter (1 dm²) und einem Quadratzentimeter (1 cm²) durchgeführt werden: Anmalen, bekleben, die Fläche mit Gegenständen auslegen, … Es gibt so viele Möglichkeiten die Fläche zu begreifen.
Nun ist es Zeit die Form zu vervielfältigen. Dazu könnt ihr zum Beispiel viele kleine Pappquadrate ausschneiden, die alle genau einen Quadratzentimeter oder einen Quadratdezimeter groß sind. Mit Hilfe dieser Quadrate lassen sich Flächen auslegen. Wählt Flächen, die für das Kind im Alltag von Bedeutung sind:
- Den Nachttisch mit Quadraten auslegen, die genau einen Quadratdezimeter groß sind
- Den Büchereiausweis mit Quadraten auslegen, die genau einen Quadratzentimeter groß sind
- Die Fläche des Spielteppichs auslegen
- Die Fläche eines Schulheftes auslegen
Zählt man die Quadrate ab, so erfährt man die genaue Größe des Gegenstandes. Passen zum Beispiel genau 40 kleine Quadrate auf den Büchereiausweis, so ist dieser 40 Quadratzentimeter groß.
Das Gleiche lässt sich theoretisch auch mit der Zimmerwand machen: Ist sie vier Meter lang und drei Meter hoch, so könnte man sie mit den ganz großen Quadraten auslegen (bzw. die Quadrate mit Stecknadeln an die Wand pinnen) und auf diese Weise feststellen, dass sie zwölf Quadratmeter groß ist. In der Praxis ist dies jedoch ziemlich aufwändig. Daher müssen wir einen anderen Weg finden!
Den Flächeninhalt eines Rechtecks berechnen
Einige Kinder kommen irgendwann von selber darauf, dass sie die Flächen eigentlich gar nicht mit Quadraten auslegen müssen, sondern die Lösung ganz einfach berechnen können indem sie die Länge der Seiten des Rechtecks miteinander multiplizieren. Sei nicht verzagt, wenn dein Kind nicht von selbst auf diese Idee kommt. Gib ihm stattdessen einen kleinen Tipp.
Gerne könnt ihr auch die Größe einiger Flächen durch beide Methoden ermitteln: Berechnet die Größe zunächst mit Hilfe der Formel A = a ⋅ b und überprüft euer Ergebnis anschließend, indem ihr die Fläche auslegt und die Quadrate abzählt.
(Eine berechtigte Frage am Rande: „Warum schreiben wir eigentlich ein großes A und nicht ein großes F für den Flächeninhalt?“ Das A geht auf das englische Wort „area“ zurück, was so viel wie „Fläche“ oder „Flächeninhalt“ bedeutet.)
Gehen wir nun zurück zur Ausgangsfrage: Also zurück in den Baumarkt, wo hunderte von Farben auf uns warten. Auf jedem Farbeimer ist eine Angabe zu finden für wie viele Quadratmeter die Farbe ausreichen wird. Wir haben die Wand vermessen, eine Skizze gezeichnet, den Flächeninhalt berechnet und können nun herausfinden welchen Farbeimer wir wählen müssen.
Auf die gleiche Art und Weise lässt sich errechnen wie viel Bodenbelag benötigt wird. Egal ob Teppichboden, Laminat oder Fliesen: In jedem Fall muss man wissen wie viel man benötigt.
Auch wenn eine Fläche im Garten mit neuem Rollrasen ausgelegt werden soll, muss man zunächst einmal den Flächeninhalt berechnen. Es gibt viele Beispiele im Alltag. Schau dich einfach mal um, welches Beispiel für euch am sinnvollsten ist.
Arbeitsblätter zum Thema
Das klingt zwar alles ganz nett, aber eigentlich hast du gar keine Zeit Pappquadrate auszuschneiden und einen solch großen Aufwand zu betreiben? In diesem Falle helfen dir vielleicht meine Arbeitsblätter „Flächeninhalt vom Rechteck berechnen – Eine Einführung“. Du findest sie wie immer auf Eduki.
Für alle, die sich bereits sicher im Thema fühlen, habe ich das folgende Arbeitsblatt vorbereitet. Ihr könnt es euch ganz einfach herunterladen und ausdrucken. Ich wünsche viel Spaß damit!
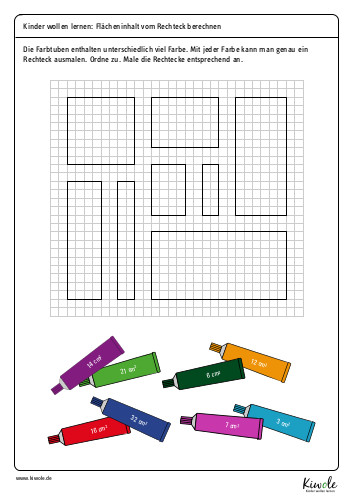
Weiterführende Aufgaben
In der Realität sind unsere Zimmer häufig verwinkelt. Darüber hinaus bilden Türen und Fenster „Löcher“ in den Wänden, welche nicht mit gestrichen werden müssen. Das Gute ist jedoch, dass eine Tür und auch ein Fenster nichts weiter als Rechtecke sind, deren Flächeninhalt wir ja bereits berechnen können. In diesem Fall würde man also den Flächeninhalt der gesamten Wand inklusive der Tür berechnen und anschließend den Flächeninhalt der Tür abziehen.
Manchmal hat der Fußboden eher die Form von einem L als von einem Rechteck. Wenn dem so ist, kann man die Fläche ganz einfach in zwei Rechtecke aufteilen (hier also den senkrechten Strich vom L und den waagerechten Strich vom L). Man berechnet den Flächeninhalt beider Rechtecke und addiert die Ergebnisse im Anschluss.
Probiert es einfach mal aus!
Knobelaufgaben
Zum Schluss habe ich noch ein paar Knobelaufgaben für diejenigen vorbereitet, die großen Spaß am Thema gefunden haben und gerne noch ein wenig weiter denken möchten:
- Eine Wand hat einen Flächeninhalt von 12 m². Die Wand ist 4 m lang. Wie hoch ist die Wand?
- Ein Quadrat hat einen Flächeninhalt von 64 cm². Wie lang sind die Seiten des Quadrats?
- Emils Zimmer ist 3 Meter lang und 4 Meter breit. Das Wohnzimmer ist doppelt so lang und doppelt so breit. In welchem Verhältnis steht der Flächeninhalt von Emils Zimmer zum Flächeninhalt des Wohnzimmers? Ist das Wohnzimmer doppelt so groß wie Emils Zimmer?
- Lia hat einen Würfel gebastelt. Die Seiten sind 10 cm lang. Nun möchte sie ihren Würfel anmalen und fragt sich wie viel Farbe sie benötigen wird. Berechne die Oberfläche des Würfels in Quadratzentimetern.
- Leon hat einen Quader gebastelt. Er ist 6 cm hoch, 4 cm breit und 8 cm lang. Leon möchte seinen Quader anmalen und fragt sich wie viel Farbe er benötigen wird. Berechne die Oberfläche des Quaders in Quadratzentimetern.
- Versuche eine Formel für die Berechnung der Oberfläche eines Würfels aufzustellen.
- Versuche eine Formel für die Berechnung der Oberfläche eines Quaders aufzustellen.
- Gegeben ist ein rechtwinkliges Dreieck. Das bedeutet, dass ein Winkel des Rechtecks genau 90° groß ist. Die Seiten des Dreieck sind 3 cm, 4 cm und 5 cm lang. Kannst du den Flächeninhalt des Dreiecks berechnen? Tipp: Eine Skizze kann dir helfen!
- Versuche eine Formel für die Berechnung des Flächeninhalts eines rechtwinkligen Dreiecks aufzustellen.
- Der Umfang eines Quadrats beträgt 40 cm. Ermittle den Flächeninhalt des Quadrats.
- Denke dir eine total verrückte Form aus, die mindestens zehn rechte Winkel hat. Zeichne sie auf und versuche ihren Flächeninhalt zu ermitteln.
Die Lösungen der Knobelaufgaben
- Die Wand ist 3 m hoch.
- Die Seiten des Quadrats sind 8 cm lang.
- Nein, das Wohnzimmer ist vier mal so groß wie Emils Zimmer.
- Die Oberfläche des Würfels ist 600 cm² groß.
- Die Oberfläche des Quaders ist 208 cm² groß.
- Die Formel für die Oberfläche eines Würfels lautet: O = 6 ⋅ a
- Die Formel für die Oberfläche eines Quaders lautet: O = 2 ⋅ a ⋅ b + 2 ⋅ a ⋅ c + 2 ⋅ b ⋅ c
- Der Flächeninhalt des Dreiecks ist 6 cm² groß.
- Die Formel für den Flächeninhalts eines rechtwinkligen Dreiecks lautet A = (a ⋅ b) : 2
- Der Flächeninhalt des Quadrats beträgt 100 cm².
Ich hoffe, meine kleine Einführung in die Welt des Flächeninhalts der Rechtecke und Quadrate konnte euch helfen! Ich wünsche euch ganz viel Spaß beim ausprobieren, begreifen, basteln, skizzieren und berechnen! Lasst mich gerne in den Kommentaren wissen wie ihr das Thema angegangen seid und was euch besonders geholfen hat!