Wer hat von meiner Schokolade genascht? Und wie viel fehlt da überhaupt? Wie gut, dass ich Brüche auf ein Ganzes ergänzen kann und mir die Lösung somit ganz schnell selber herleiten kann.
Meine Tafel Schokolade besteht aus 24 Stücken. Jeweils vier Stücke bilden zusammen einen Riegel. Jemand hat genau einen Riegel verputzt. Es fehlt also einer von sechs Riegeln. Anders ausgedrückt: Es fehlt ein Sechstel meiner Schokolade!
Wie viel Schokolade bleibt mir denn nun noch? Fünf Riegel sind noch übrig. Mir bleiben also fünf Sechstel.
Mathematisch ausgedrückt könnte man es so umschreiben: 1/6 + 5/6 = 1 (Das fehlende Sechstel plus die fünf verbleibenden Sechstel ergeben zusammen eine ganze Tafel Schokolade.)
Arbeitsblatt „Brüche auf ein Ganzes ergänzen“
Wenn man sich anschaulich vor Augen hält wie viel vom Ganzen fehlt, ist es ein Kinderspiel Brüche auf ein Ganzes zu ergänzen. Ihr könnt hierzu Schokolade, Süßigkeiten oder Kuchen verwenden. Zur Unterstützung habe ich euch darüber hinaus ein paar Arbeitsblätter vorbereitet. Einige findet ihr auf eduki. Eines stelle ich euch gleich hier zur Verfügung:
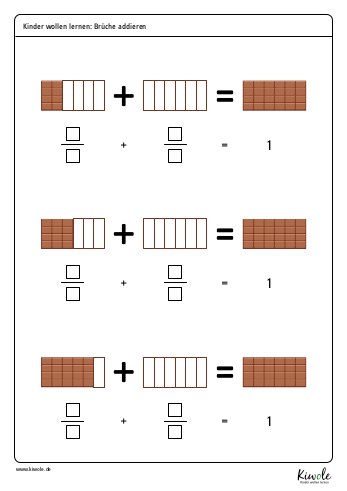
Nachdem wir das Problem anschaulich gelöst haben, kommt hier die mathematische Erklärung:
Die Zahl 1 lässt sich alternativ als Bruch darstellen, dessen Zähler und Nenner gleich groß sind. So ist zum Beispiel 3/3 gleich 1. Im oben genannten Beispiel könnten wir die 1 in 6/6 umwandeln.
Wollen wir Brüche addieren, so behalten wir den Nenner bei und addieren die beiden Zähler miteinander. (Eine ausführliche Erklärung hierzu findet ihr in meinem Artikel „Einführung in die Bruchrechnung„.) Wollen wir nun also 1/6 zum Ganzen ergänzen, so machen wir uns zunächst klar, dass ein Ganzes 6/6 entspricht. Wir stehen also mathematisch gesehen vor der Aufgabe 1/6 plus wie viel ist 6/6?
Der Nenner wird beibehalten. So können wir uns gänzlich auf die Zähler konzentrieren: 1 plus wie viel ist 6? Diese Aufgabe haben wir bereits in der ersten Klasse gelöst. Die Antwort lautet natürlich 5.
Setzen wir Zähler und Nenner nun wieder zusammen, so erhalten wir 5/6.
Alles klar? Dann kann ich nun in Ruhe meine Schokolade naschen. Mittlerweile sind es schon nur noch zwei Sechstel. Hm, lecker…



