Wie findet man den kürzesten Abstand zwischen einem Punkt und einer Geraden? Lass uns das Problem einmal anhand eines anschaulichen Beispiels betrachten:
Anschauliches Beispiel
Stell dir vor, du bist an einem großen See. Plötzlich gerät eine Person in Not und muss sofort gerettet werden! Du läufst am Ufer entlang und suchst die Stelle, an der der Abstand zwischen dir und der in Not geratenen Person am geringsten ist. Die Strecke, welche du schwimmen musst, sollte möglichst gering sein, damit du schnell am Ziel ankommst. Wo musst du ins Wasser gehen?
Lass uns die oben gezeigte Situation vereinfacht darstellen:
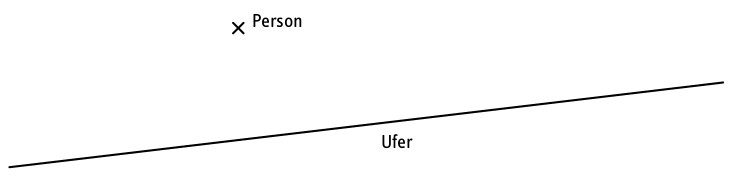
Je nachdem an welcher Stelle du ins Wasser gehst, verlängert oder verkürzt sich der Weg zur in Not geratenen Person. Vielleicht ist es dir beim gedanklichen Ausprobieren bereits aufgefallen: Wenn du eine zur Ausgangsgeraden senkrechte Strecke zeichnest, die durch den gegebenen Punkt geht, so erhältst du die kürzeste Strecke zwischen dem Punkt und der Geraden.
Das klingt erst einmal kompliziert, aber wenn wir uns ein Bild zur Hilfe nehmen, wird die Sache schnell klarer:
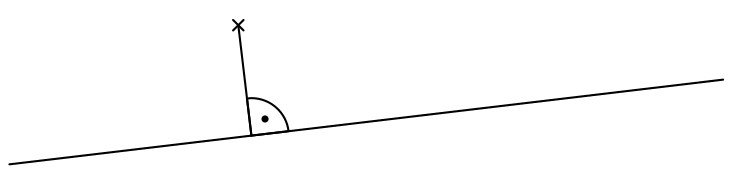
Für die praktische Umsetzung nutze dein Geodreieck. Lege die Mittellinie deines Geodreiecks auf die Gerade. Schiebe das Geodreieck anschließend so lange an der Geraden entlang, bis du den gegebenen Punkt erreichst. Nun kannst du die Senkrechte einzeichnen und – wenn gefordert – ihre Länge messen.
Übungen zum Thema „Abstand Punkt Gerade“
Alles klar? Probiere es doch gleich einmal aus! Alles was du brauchst ist ein spitzer Bleistift und ein Geodreieck. Zeichne eine Gerade und einen beliebigen Punkt. Versuche nun, den kürzesten Abstand zwischen Punkt und Gerade zu ermitteln. Viel Erfolg dabei!
Wenn du weitere Übungen zu diesem Thema machen möchtest, schau dir gerne mal meine Arbeitsblätter zum Thema „Abstand Punkt Gerade“ auf eduki an!
