Hier siehst du einen Quader. In meinem Blogartikel „Schrägbilder geometrischer Körper zeichnen“ hast du bereits gelernt, wie du einen Quader auf kariertem Papier zeichnen kannst. Heute zeige ich dir, wie du die Quaderoberfläche berechnen kannst.
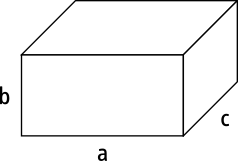
Der Aufbau eines Quaders
Schau dir das Bild des Quaders noch einmal genau an. Vielleicht magst du dir auch einen quaderförmigen Gegenstand holen und diesen in Ruhe von allen Seiten betrachten. Hierzu eignet sich zum Beispiel der Karton einer Müsliverpackung oder eine Streichholzschachtel.
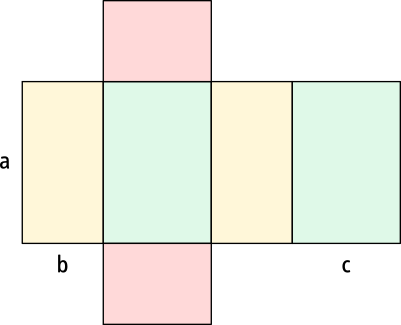
Du siehst: Ein Quader hat zwölf Kanten, acht Ecken und sechs Flächen. Jeweils zwei dieser Flächen sind gleich groß. Besonders gut ist dies am Quadernetz erkennbar. Denn sein Netz besteht aus sechs rechteckigen Flächen, wobei jeweils zwei gleich groß sind. Ich habe sie hier zur Veranschaulichung in den gleichen Farben dargestellt.
Die Längen der Kanten werden üblicherweise als a, b und c bezeichnet.
Berechnung der Quaderoberfläche
Erinnerst du dich noch daran, wie der Flächeninhalt eines Rechtecks berechnet wird? Dieses Grundwissen ist Voraussetzung für die folgenden Schritte. Solltest du dich nicht daran erinnern, lies bitte zunächst noch einmal meinen Blogartikel „Flächeninhalt vom Rechteck“ genau durch.

Die Formel für den Flächeninhalt eines Rechtecks lautet: A = a ⋅ b
Die Oberfläche eines Quaders ist die Summe der Flächen aller sechs Seiten. Gehen wir es Schritt für Schritt durch: Der Quader besteht aus sechs rechteckigen Flächen, wobei jeweils zwei gleich groß sind. Der Flächeninhalt des ersten Rechtecks kann mit der Formel A = a ⋅ b berechnet werden, der Flächeninhalt des zweiten Rechtecks mit der Formel A = a ⋅ c und derjenige des dritten Rechtecks mit der Formel A = b ⋅ c. Daraus ergibt sich die Formel für die gesamte Quaderoberfläche: O = 2ab + 2ac + 2bc
Arbeitsblätter
Probiere es aus. Für den Anfang fällt es dir vielleicht leichter, wenn du statt eines Quaders das Quadernetz betrachtest. So erinnerst du dich schnell an die Formel zur Berechnung der Quaderoberfläche. Hierzu habe ich dir ein Arbeitsblatt vorbereitet, das du dir gerne direkt herunterladen und ausdrucken kannst.
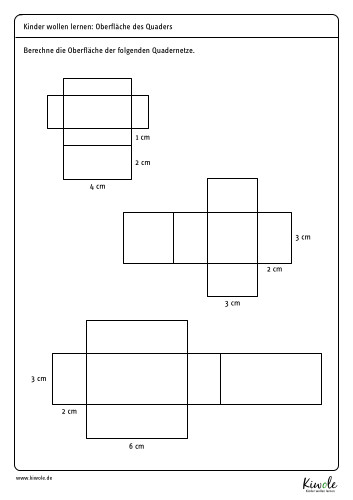
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Weitere Arbeitsblätter findest du in meinem Material „Einführung Quaderoberfläche – Die Oberfläche des Quaders berechnen“ auf Eduki. Ich wünsche dir viel Spaß damit!
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)