Die Punktsymmetrie ist ein Teilgebiet der Drehsymmetrie. Zur Erinnerung könnt ihr euch gerne noch einmal meinen Artikel „Einführung in die Drehsymmetrie“ anschauen. Eine Figur ist drehsymmetrisch, wenn man sie drehen kann und sie sich dabei auf sich selbst abbildet. Punktsymmetrisch ist sie hingegen, wenn sie sich bei einer Drehung von exakt 180° auf sich selbst abbildet.
Anschauliche Beispiele
Nehmt euch ein handelsübliches Kartenspiel zur Hand. Wir alle wissen, dass darauf irgendwie Karo, Herz, Pik und Kreuz zu sehen sind. Doch wie ist so eine Karte eigentlich im Detail aufgebaut? Schaut es euch an! Das verblüffende an diesen Karten ist, dass man sie niemals falsch herum halten kann. Egal wie man sie auch dreht und wendet, sie stehen niemals auf dem Kopf. Dies ist der Punktsymmetrie geschuldet, denn alle Elemente auf der Karte – egal ob Zahlen, Symbole und Illustrationen – bilden sich bei einer Drehung von 180° wieder auf sich selbst ab.
Punktsymmetrie versteckt sich auch in vielen geometrischen Formen. Zum Beispiel in einigen Vierecken. Überlegt einmal… welche Vierecke fallen euch ein, die punktsymmetrisch sind?
Na, habt ihr welche gefunden? Genau! Alle Parallelogramme sind punktsymmetrisch! Und da es sich bei einem Quadrat, einem Rechteck und einer Raute um spezielle Parallelogramme handelt, sind natürlich auch diese punktsymmetrisch.
Wenn ihr Spaß an Knobelaufgaben dieser Art habt, macht euch doch mal Gedanken darüber, ob die folgenden geometrischen Figuren ebenfalls punktsymmetrisch sind: Kreise, Dreiecke, Fünfecke, Sechsecke, Siebenecke, Achtecke. Einige der eben genannten sind nur unter bestimmten Voraussetzungen punktsymmetrisch. Findet ihr sie? Und wie verhält es sich mit einer Geraden und einer Strecke? Sind sie ebenfalls punktsymmetrisch und wo liegt ihr Symmetriepunkt? Könnt ihr auch den Symmetriepunkt im Parallelogramm finden? Wie könnte man vorgehen?
Arbeitsblätter zur Punktsymmetrie
Wie immer habe ich euch ein Arbeitsblatt vorbereitet, welches ihr euch hier kostenlos herunterladen könnt.
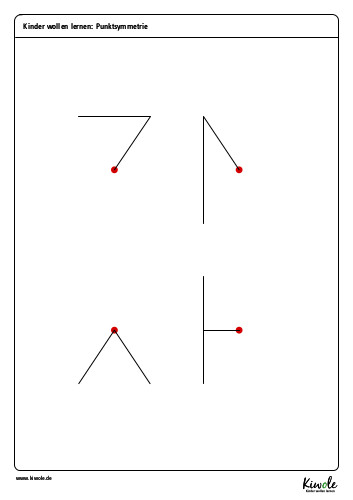
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Weitere Arbeitsblätter zum Thema Punktsymmetrie findet ihr auf eduki. Ich wünsche euch viel Spaß damit!
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)