Die Kombinatorik ist ein Teilgebiet der Stochastik. Sie wird bereits in der Grundschule eingeführt und später auf der weiterführenden Schule vertieft.
Beispiele
Kombinatorische Aufgaben können uns überall im Alltag begegnen. Hier einige Beispiele:
- Stell dir vor, du stehst vor deinem Kleiderschrank. Darin liegen zwei Hosen und drei Pullover. Du hast die Qual der Wahl. Welches Outfit ist für heute das Richtige? Und wie viele Kombinationsmöglichkeiten hast du überhaupt? (Die Lösung findest du weiter unten.)
- Du stehst in der Eisdiele und bestellst zweimal Schokolade und einmal Vanille in der Waffel. In welcher Reihenfolge könnte der Eismann die Kugeln in die Waffel schichten? Wie viele Kombinationsmöglichkeiten gibt es?
- Du möchtest Plätzchen backen. In der Backschublade findest du zwei Plätzchenformen: Eine Herzform und eine Sternform. Außerdem hast du zwei Glasuren zur Auswahl: Gelb und rot. Ganz hinten in der Schublade findest du noch Streusel. Du beschließt, dass alle Plätzchen eine Glasur bekommen sollen, aber nur einige zusätzlich dazu noch Streusel. Wie viele unterschiedliche Plätzchen kannst du backen?
Einführung in die Kombinatorik
Konntest du alle Rätsel lösen? Hat es dir vielleicht sogar Spaß gemacht? Wie bist du vorgegangen? Hast du die unterschiedlichen Möglichkeiten ausprobiert oder bist du systematisch vorgegangen?
Die meisten Kinder lösen Rätsel dieser Art anfangs durch ausprobieren. Das ist auch völlig in Ordnung. Erst wenn die Rätsel durch noch mehr Kombinationsmöglichkeiten komplexer werden oder die Kinder bereits Erfahrungen mit solchen Aufgaben gesammelt haben, beginnen sie sich eigene Strategien zurechtzulegen. An dieser Stelle möchte ich betonen, dass wir es nach Möglichkeit unterlassen sollten den Kindern unsere Lösung aufzuzwingen. Häufig finden sie ganz eigene Arten der Ordnung und kommen so sehr gut ans Ziel.
Aufgaben aus dem Alltag
Wenn du dich mit deinem Kind zu Hause mit der Kombinatorik beschäftigen möchtest, so biete einfach eine Aufgabe aus dem Alltag an. Zum Beispiel die oben genannte Aufgabe mit den Kleidungsstücken. Diese lässt sich einfach variieren, indem mehr oder andere Kleidungsstücke hinzugenommen werden. Außerdem haben die Kleidungsstücke den großen Vorteil, dass man die Lösungen direkt durch Legen ausprobieren kann.
Eine andere Möglichkeit sind Perlen, die in unterschiedlichen Reihenfolgen aufgefädelt werden können. Nimm beispielsweise eine rote, eine rosafarbene und eine lilane Perle. Wie viele unterschiedliche Reihenfolgen findet ihr diese drei Perlen aufzufädeln? (Die Lösung zu diesem Problem findest du unten unter Punkt 4.) Um die Aufgabe etwas schwieriger zu machen, kannst du eine weitere Farbe hinzu nehmen. Was passiert, wenn du statt einer neuen Farbe eine der vorhandenen Farben doppelt nimmst?
Wer Perlen nicht mag, kann natürlich auch verschiedenfarbige Schokolinsen in eine Reihe legen oder unterschiedlich farbige Bauklötze zu einem Turm stapeln.
Es lassen sich wirklich viele Dinge im Alltag finden. Sie alle haben gemeinsam, dass sie für das Kind begreifbar sind. Außerdem lassen sich die Aufgaben beliebig erweitern und dem Kenntnisstand des Kindes anpassen. Alle oben genannten Aufgaben entsprechen dem Niveau der Aufgaben, welche in der Grundschule besprochen werden. Wenn ihr mögt, könnt ihr eure Ergebnisse zu Papier bringen. Manchmal ist es einfacher herauszufinden, ob man eine bestimmte Kombinationsmöglichkeit bereits hatte, wenn man auf dem Papier nachsehen kann. (Hierzu muss das Kind übrigens weder Zahlen noch Buchstaben kennen. Es kann die Lösungen einfach aufmalen.)
Systematisches Vorgehen mit Hilfe einer Tabelle
Wie oben bereits angedeutet gibt es neben der Möglichkeit des Ausprobierens auch systematische Vorgehensweisen zur Lösung kombinatorischer Problemstellungen. Sehen wir uns zunächst einmal die Tabelle an.
Im folgenden Beispiel gehen wir davon aus, dass Juna rote, gelbe und blaue Bausteine zur Verfügung hat, aus denen sie einen kleinen Turm bauen möchte. Ihr Turm besteht aus einer Brücke und einem würfelförmigen Stein. Wie könnte dieser Turm aussehen? Schaut euch einmal die Tabelle auf dem folgenden Arbeitsblatt an!
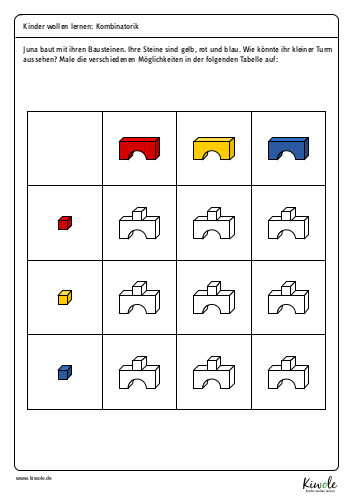
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Als Erwachsene sehen wir hier mit nur einem Blick, dass es neun verschiedene Möglichkeiten gibt. Kindern geht es ähnlich. Nachdem sie einmal alle Kombinationsmöglichkeiten auf dem Arbeitsblatt angemalt haben, werden sie das System in der nächsten Tabelle direkt wiedererkennen. Mit einiger Übung werden sie dann selber in der Lage sein eigene Tabellen zu ähnlichen Problemstellungen zu erarbeiten.
Hier einige Vorschläge (die Lösungen findest du weiter unten):
- Es ist kalt draußen. Leon hat eine blaue und eine grüne Mütze sowie einen blauen und einen grünen Schal. Er kann sich nicht entscheiden, welchen Schal und welche Mütze er anziehen soll. Wie viele Kombinationsmöglichkeiten hat er?
- Marie kocht Pudding. Sie hat Schokopudding und Vanillepudding zur Auswahl. Obst soll ihren Pudding verzieren. Sie könnte Bananenscheiben, Kirschen oder Weintrauben verwenden. Wie viele Möglichkeiten hat Marie?
- Jana möchte sich ganz verrückt verkleiden. Sie hat eine Krone, einen Cowboyhut, einen Zylinder und einen Strohhut als mögliche Kopfbedeckungen. Außerdem liegt ein Prinzessinnenkleid, ein Zauberumhang, ein Meerjungfrauenkostüm und eine Ritterrüstung vor ihr. Wie viele Kombinationsmöglichkeiten hat sie, wenn sie genau eine Kopfbedeckung mit einem Kostüm verbinden möchte?
Das Baumdiagramm
Das Baumdiagramm bietet eine weitere Möglichkeit des systematischen Vorgehens. Schau dir einmal das folgende Baumdiagramm an:

Als erstes steht die Entscheidung für eine gold-gelbe oder eine rote Schleife an. Danach können wir uns für ein Geschenkpapier entscheiden: Grün, rot oder dunkelblau. Wir haben also auf der ersten Ebene zwei Entscheidungsmöglichkeiten und auf der zweiten Ebene drei Möglichkeiten. Am Ende erhalten wir sechs verschiedene Kombinationen.
Tatsächlich können wir das Ergebnis auch berechnen. Hierzu multiplizieren wir die Möglichkeiten der ersten Ebene mit den Möglichkeiten der zweiten Ebene. In diesem Fall ergibt sich: 2∙3=6
Natürlich kann ein Baumdiagramm noch viele weitere Ebenen haben. Es eignet sich also hervorragend um komplexe Probleme anschaulich zu machen. Sehen wir uns dazu einige Beispiele an. Die dazugehörigen Lösungen findest du natürlich wie immer am Ende dieses Beitrags.
- Noah sichert sein Fahrrad mit einem Zahlenschloss. Seine Geheimzahl besteht aus vier Ziffern. Möglich sind die Ziffern von 0 bis 9. Wie viele Kombinationsmöglichkeiten gibt es? (Zur Vereinfachung kann man die Geheimzahl zunächst auf zwei oder drei Ziffern begrenzen. Außerdem ist es möglich nur Ziffern von 0 bis 5 zuzulassen.)
- Lilli geht mit ihren Eltern in ein Restaurant. Als Vorspeise kann sie zwischen einer Gemüsesuppe und einer Tomatensuppe wählen. Als Hauptgerichte stehen Nudeln mit Tomatensoße, Pizza, Kartoffelsalat mit Würstchen und Pommes mit Schnitzel zur Auswahl. Zum Nachtisch kann sie zwischen Erdbeereis mit Sahne, Waffeln mit heißen Kirschen und Schokopudding wählen. Wie viele Kombinationsmöglichkeiten hat Lilli?
Arbeitsblätter zum Thema Kombinatorik
Nun hast du schon sehr viele unterschiedliche Aufgaben kennen gelernt und erste Ideen an die Hand bekommen, wie du die Aufgaben systematisch lösen kannst. Weitere Arbeitsblätter zum Thema Kombinatorik findest du wie immer auf eduki:
Lösungen zu den oben genannten Beispielen
Hier findest du alle Lösungen zu den oben beschriebenen Problemen:
- Du hast sechs verschiedene Outfits zur Auswahl:
- Hose 1 + Pullover 1
- Hose 1 + Pullover 2
- Hose 1 + Pullover 3
- Hose 2 + Pullover 1
- Hose 2 + Pullover 2
- Hose 2 + Pullover 3
- Der Eismann hat drei Möglichkeiten:
- Schokolade – Schokolade – Vanille
- Schokolade – Vanille – Schokolade
- Vanille – Schokolade – Schokolade
- Du kannst acht unterschiedliche Plätzchen backen:
- Herz + gelbe Glasur ohne Streusel
- Herz + gelbe Glasur + Streusel
- Herz + rote Glasur ohne Streusel
- Herz + rote Glasur + Streusel
- Stern + gelbe Glasur ohne Streusel
- Stern + gelbe Glasur + Streusel
- Stern + rote Glasur ohne Streusel
- Stern + rote Glasur + Streusel
- Es gibt sechs verschiedene Reihenfolgen:
- rot – rosa – lila
- rot – lila – rosa
- lila – rot – rosa
- lila – rosa – rot
- rosa – lila – rot
- rosa – rot – lila
- Leon hat vier Kombinationsmöglichkeiten:
- blaue Mütze + blauer Schal
- blaue Mütze + grüner Schal
- grüne Mütze + blauer Schal
- grüne Mütze + grüner Schal
- Marie hat sechs verschiedene Möglichkeiten:
- Schokopudding + Bananenscheiben
- Schokopudding + Kirschen
- Schokopudding + Weintrauben
- Vanillepudding + Bananenscheiben
- Vanillepudding + Kirschen
- Vanillepudding + Weintrauben
- Jana hat 16 verschiedene Outfits zur Auswahl:
- Prinzessinnenkleid + Krone
- Prinzessinnenkleid + Cowboyhut
- Prinzessinnenkleid + Zylinder
- Prinzessinnenkleid + Strohhut
- Zauberumhang + Krone
- Zauberumhang + Cowboyhut
- Zauberumhang + Zylinder
- Zauberumhang + Strohhut
- Meerjungfrauenkostüm + Krone
- Meerjungfrauenkostüm + Cowboyhut
- Meerjungfrauenkostüm + Zylinder
- Meerjungfrauenkostüm + Strohhut
- Ritterrüstung + Krone
- Ritterrüstung + Cowboyhut
- Ritterrüstung + Zylinder
- Ritterrüstung + Strohhut
- Das Zahlenschloss hat 10.000 mögliche Kombinationen. Man kann alle Zahlen von 0000 bis 9999 einstellen. Wenn man ein Baumdiagramm zur Lösung des Problems benutzt, so hat man auf jeder Entscheidungsebene 10 Möglichkeiten (0, 1, 2, 3, 4, 5, 6, 7, 8 oder 9). Da es vier Entscheidungsebenen gibt, erhalten wir die folgende Rechnung: 10∙10∙10∙10=10.000
- Lilli kann zwischen 24 Menüs wählen. Im Baumdiagramm stehen auf der ersten Entscheidungsebene zwei Suppen, auf der zweiten Entscheidungsebene vier verschiedene Hauptgerichte und auf der dritten Ebene drei Nachspeisen. Daraus ergibt sich folgende Rechnung: 2∙4∙3=24
Na, konntest du alle Aufgaben richtig lösen?
Ich hoffe, unser kleiner Ausflug in die Kombinatorik hat dir Spaß gemacht! Berichte mir doch gerne in den Kommentaren welches Rätsel für dich am kniffligsten war und welches du am liebsten mochtest! Ich würde mich freuen…
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)