Habt ihr meinen Artikel zur Parallelperspektive noch im Kopf? Kurz zur Erinnerung: Bei der parallperspektivischen Darstellung werden alle Linien, die in der Wirklichkeit parallel zueinander verlaufen, auch auf dem Papier parallel dargestellt. Auf die Verwendung von Fluchtpunkten wird vollständig verzichtet. Heute widmen wir uns der Isometrie, einem Teilgebiet der Parallelperspektive.
Was ist das Besondere bei der Isometrie?
Isometrie bedeutet Längengleichheit oder Längentreue. Bei der isometrischen Axonometrie werden die Linien nicht verkürzt wie in anderen perspektivischen Darstellungen. Besonders anschaulich wird dies, wenn wir einen Würfel betrachten. Bekanntlich sind bei einem Würfel alle Seiten gleich lang. Ebenso ist es in unserer isometrischen Darstellung! Du kannst gerne auf dem folgenden Arbeitsblatt nachmessen. Alle Seiten des Würfels sind gleich lang.
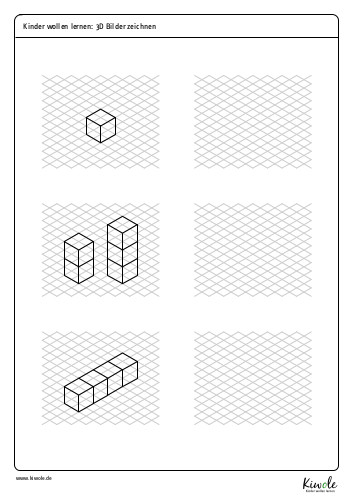
Wir erreichen dies, indem wir die Seiten des Objekts im Winkel von 30° zur Grundlinie zeichnen. Ich empfehle euch daher ein Hilfslinienraster zu zeichnen, in dem alle Linien um 30° gekippt sind. Als Vorlage können euch die Hilfslinien auf dem Arbeitsblatt dienen.
Einfache Objekte zeichnen
Um sich mit dieser ungewohnten Darstellung vertraut zu machen, ist es ratsam anfangs einige Würfel zu zeichnen. Im Anschluss können die Würfel zu kleinen Gebäuden kombiniert werden, indem du sie stapelst oder einige nebeneinander zeichnest. Versuche kleinere und größere Würfel auf das Papier zu bringen. Gelingt es dir kompliziertere Gebilde wie einen Tunnel oder einen Tisch zu zeichnen? Versuche einmal eine Treppe! Du könntest die Möbel deines Zimmers darstellen. Oder dich als Architekt an ungewöhnliche Gebäudekonstruktionen herantrauen! Probiere es einfach mal aus!
Weitere Arbeitsblätter dieser Art findest du wie immer auf eduki:
- Einführung Isometrie – Wir zeichnen isometrische Bilder
- Isometrie Teil 2 – Wir zeichnen isometrische Bilder
- Isometrie – 3D Muster abzeichnen
Viel Spaß damit!