In der Vergangenheit habe ich schon oft über verschiedene Aspekte der Achsensymmetrie geschrieben. Für den Einstieg empfehle ich dir meine Blogartikel „Achsensymmetrie durch spiegeln begreifen„, „Symmetrische Figuren vervollständigen“ sowie „Spiegelbilder im Gitternetz„. Fortgeschrittene finden Anregungen in meinem Blogartikel „Achsensymmetrie im Koordinatensystem„. Auch mein heutiges Thema „Doppelspiegelung an parallelen Achsen“ richtet sich an die Fortgeschrittenen.
Was ist eine Doppelspiegelung an parallelen Achsen?
Bei der einfachen Spiegelung spiegelst du jeden Punkt an einer vorgegebenen Spiegelachse. Bei der Doppelspiegelung hingegen spiegelst du jeden Punkt zuerst an einer Achse und anschließend an einer zweiten Achse.
Heute betrachte ich nur den Sonderfall „Doppelspiegelung an parallelen Achsen“, bei dem die beiden Spiegelachsen parallel zueinander liegen.
Die Doppelspiegelung erweist sich als relativ simpel, wenn du zunächst wie bei der Achsenspiegelung gewohnt alle Punkte an der ersten Achse spiegelst. Ignoriere die zweite Achse so lange. Sind alle Punkte und Linien exakt übertragen, so widme dich der zweiten Achse. Spiegele nun deine erste Spiegelung an der zweiten Achse. Achte darauf, dass du die Punkte tatsächlich spiegelst und nicht aus Versehen nur um eine bestimmte Anzahl an Kästchen verschiebst.
Mathematische Gedanken
Eine interessante Eigenschaft der Doppelspiegelung an parallelen Achsen ist, dass sie eine Verschiebung des ursprünglichen Objekts bewirkt. Der Abstand zwischen den beiden Spiegelachsen bestimmt dabei die Verschiebungsrichtung und -größe des Objekts. Wenn wir den Abstand zwischen den beiden Achsen als a bezeichnen, dann wird das gesamte Objekt bei einer Doppelspiegelung um 2a in Richtung der zweiten Achse verschoben.
Arbeitsblätter
Wie immer habe ich dir auch heute Arbeitsblätter zum Thema mitgebracht. Das erste kannst du dir gerne direkt hier herunterladen und ausdrucken:
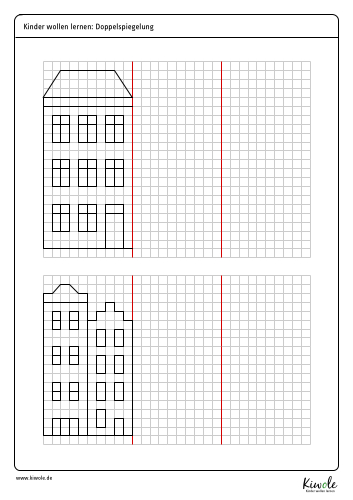
(Downloads und Kopien sind nur für den privaten Gebrauch gestattet. Weitere Informationen (auch zur kommerziellen Nutzung) findest du hier.)
Weitere Arbeitsblätter zur Doppelspiegelung findest du auf eduki. Hier ist übrigens auch die Lösung des oben gezeigten Arbeitsblattes hinterlegt. Schau gerne mal rein und überprüfe, ob du alles richtig gemacht hast!
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)