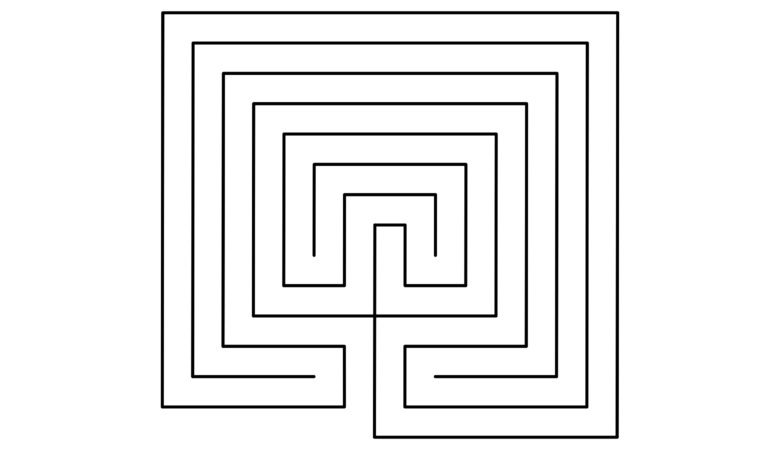
Alle Kinder kennen Irrgärten. Sie lieben es den Weg vom Start bis zum Ziel zu finden, wobei Abzweigungen und Sackgassen zu Verwirrungen führen können. Ein echtes Geduldsspiel! Fälschlicherweise wird der Irrgarten häufig als „Labyrinth“ bezeichnet. Dabei besteht das klassische Labyrinth aus nur einem einzigen Pfad. Dieser Pfad kann sind in vielen Windungen schlängeln, aber es …