Das Wort „Blütenaufgabe“ erweckt den Anschein als befänden wir uns im Bereich des Biologieunterrichts. Doch weit gefehlt. Blütenaufgaben sind Teil des Mathematikunterrichts.
Was sind Blütenaufgaben?
Im Mathematikunterricht werden unterschiedliche Aufgabentypen verwendet. Die Bekanntesten sind die Beispielaufgaben, die Grundaufgaben und die Umkehraufgaben. Diese Aufgabentypen findet man in jedem Mathematikbuch. Es handelt sich hierbei um ganz oder teilweise geschlossene Aufgaben. Dem gegenüber stehen teilweise geöffnete oder offene Aufgaben.
Offene und geschlossene Aufgaben nach Regina Bruder
Die Mathematikdidaktikerin und Hochschullehrerin Regina Bruder hat eine Aufgabentypisierung vorgenommen. Sie unterscheidet bei einer Aufgabe die drei Komponenten
- Anfangssituation (Gegebenes)
- Transformationen (Lösungsweg(e))
- Endsituation (Ziel)
Der Einfachheit halber werde ich die Komponenten im Folgenden als „Start“, „Weg“ und „Ziel“ bezeichnen.
Ist eine Komponente bekannt oder vorgegeben, so wird diese mit einem „x“ gekennzeichnet. Ist sie hingegen unbekannt, so wird sie mit einem „-“ gekennzeichnet. Hieraus lässt sich nachstehende Tabelle ableiten:
| Start | Weg | Ziel | |
|---|---|---|---|
| Beispielaufgabe | x | x | x |
| Grundaufgabe | x | x | – |
| Umkehraufgabe | – | x | x |
| Problemaufgabe | x | – | – |
| offene Aufgabe | – | – | – |
Bei einer Beispielaufgabe sind Start, Weg und auch Ziel gegeben. Die Schülerinnen und Schüler können die Aufgabe lediglich passiv nachvollziehen. Er handelt sich um eine maximal geschlossene Aufgabe.
Sind sowohl Start als auch der Weg vorgegeben, so handelt es sich um eine Grundaufgabe, wie wir sie massenhaft in Mathematikbüchern für die Grundschule wie auch für die weiterführende Schule finden. Sind der Lösungsweg und das Ziel gegeben, so handelt es sich um eine klassische Umkehraufgabe.
Bei der Problemaufgabe hingegen ist nur die Anfangssituation gegeben. Den Schülerinnen und Schülern wird bei diesem Aufgabentyp ermöglicht ihren individuellen Lösungsweg zu finden. Ebenso ist es denkbar, dass nur der Weg oder nur das Ziel vorgegeben ist.
Eine vollkommen geöffnete Aufgabe gibt weder den Start, noch den Weg oder das Ziel vor. In der Aufgabenstellung wird nur ein grober Rahmen oder eine Orientierung gegeben. Die Schülerinnen und Schüler können anhand dieser Fragestellung Start, Weg und Ziel selbständig entwickeln.
Die vollständige Aufgabentypisierung ist nachzulesen in „Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung – Wege zu einem anspruchsvollen Mathematikunterricht für alle“ von Regina Bruder. Hier ist darüber hinaus zu jedem Aufgabentyp eine Beispielaufgabe zu finden.
Das Blütenmodell nach Hans Schupp
Die Grundidee zur Blütenaufgabe geht auf den Mathematiker Hans Schupp zurück. Eine Blütenaufgabe besteht aus zunehmend anspruchsvolleren Teilaufgaben unterschiedlicher Aufgabentypen. Während es sich bei der ersten Teilaufgabe noch um eine geschlossene Aufgabe handelt, öffnen sich die nachfolgenden Teilaufgaben mit steigender Tendenz. Dies assoziierte Schupp mit dem Öffnen einer Blüte. Daher der Name „Blütenaufgaben“. Alle Teilaufgaben beziehen sich dabei auf ein gemeinsames Oberthema. (vgl. Schupp, 2003)
Ein Beispiel für eine Blütenaufgabe
Eine Blütenaufgabe aus dem Bereich der Achsensymmetrie könnte demnach wie folgt aussehen:
- Spiegele das Bild.
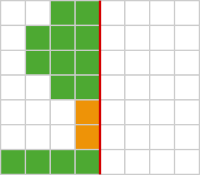
- Finde den Fehler. Erkläre, warum das Bild nicht richtig gespiegelt wurde.
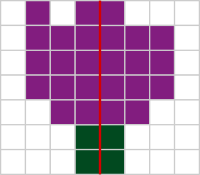
- Wo begegnet dir Symmetrie in der Natur?
- Zeichne eine symmetrische Blüte.
Diese Blütenaufgabe beginnt mit einer klassischen, geschlossenen Aufgabe. Der Start und der Weg sind vorgegeben. Die Schülerinnen und Schüler müssen das vorgegebene Bild wie gewohnt spiegeln und aufmalen. Ähnliche Aufgaben sind ihnen bereits im Vorfeld bei der Erarbeitung des Themas begegnet.
Bei der zweiten Teilaufgabe handelt es sich um eine Begründungs- oder Beweisaufgabe. Sowohl der Start als auch das Ziel sind gegeben. Es fehlt lediglich der Weg.
Die dritte Teilaufgabe ist eine Problemaufgabe, bei der lediglich der Start gegeben ist. Die Schülerinnen und Schüler können eigenständig nach einem Lösungsweg suchen. Es ist beispielsweise denkbar, dass sie nach draußen gehen um dort nach symmetrischen Pflanzen Ausschau zu halten. Auch das Ziel ist nicht vorgegeben. Die Schülerinnen und Schüler könnten die gefundenen Pflanzen fotografieren. Ebenso ist es denkbar, dass sie im Internet nach geeigneten Pflanzen und Tieren suchen und ihre Ergebnisse anschließend ausdrucken.
Als letzte Teilaufgabe finden die Schülerinnen und Schüler eine vollständig geöffnete Aufgabe vor. Sie sollen eine eigenständige symmetrische Zeichnung entwerfen. Der Schwierigkeitsgrad kann hier frei gewählt werden anhand der Größe der Zeichnung, der Anzahl der verwendeten Farben, der Detailliertheit der Zeichnung usw.
Variationen
Ausgehend von der Grundidee des Blütenmodells nach Hans Schupp sind einige Variationen möglich. Die erste Fragestellung lautet, aus wie vielen Teilaufgaben eine Blütenaufgabe idealerweise bestehen sollte. In der Literatur sind unterschiedliche Angaben zu finden. In der Regel werden drei bis fünf Teilaufgaben empfohlen. Es gibt jedoch auch weit darüber hinausgehende Blütenaufgaben mit bis zu zehn Teilaufgaben.
Das ursprüngliche Blütenmodell geht davon aus, dass sich die Aufgabe von Teilaufgabe zu Teilaufgabe immer weiter öffnet. Dies birgt die Gefahr, dass die Schülerinnen und Schüler davon ausgehen, dass sich der Schwierigkeitsgrad von Teilaufgabe zu Teilaufgabe steigert. Um dem entgegen zu wirken, könnten die Teilaufgaben in beliebiger Reihenfolge angeboten werden. Statt sie wie gewohnt durchzunummerieren, könnte man sie mit Farben oder mit Spielkartensymbolen (Kreuz, Pik, Herz und Karo) kennzeichnen. Nähere Informationen zu dieser Idee finden sich in „Differenzierter Unterricht mit Blütenaufgaben“ von Alexander Salle, Rudolf vom Hofe und Andreas Pallack. In ihrer Studie kommen sie zu folgendem Fazit: „Die untersuchten Schülerinnen und Schüler unterscheiden sich hochgradig bei der Schwierigkeitsbewertung der Teilaufgaben und begründen dies mit vielfältigen Argumenten. Weiterhin befürworten sie die freie Aufgabenauswahl und sprechen sich größtenteils gegen eine hierarchische Anordnung aus.“ (Roth & Ames, 2014)
Wie kann ich Blütenaufgaben im Mathematikunterricht einsetzen?
Der Einsatz von Blütenaufgaben eignet sich insbesondere in der Phase des vertiefenden Lernens.
In der Literatur finden sich unterschiedliche Empfehlungen zum konkreten Einsatz von Blütenaufgaben. So ist es beispielsweise möglich den Schülerinnen und Schülern einen festen Zeitrahmen von 15 oder 20 Minuten zu setzen in denen sie so weit wie möglich kommen sollen. Auf diese Weise lernt jeder Schüler und jede Schülerin in seinem bzw. ihrem individuellen Lerntempo. Es ist nicht das Ziel, am Ende alle Aufgaben bearbeitet zu haben.
Eine andere Herangehensweise erlaubt den Schülerinnen und Schülern einfachere Aufgaben zu überspringen. Ebenso ist es denkbar, dass sich die Schülerinnen und Schüler die zu bearbeitenden Teilaufgaben vollkommen frei aussuchen dürfen. Hierbei könnte eine Vorgabe bezüglich der Menge der mindestens zu erledigenden Teilaufgaben gemacht werden. Auch ist es möglich den Schwierigkeitsgrad der Teilaufgaben durch ein Punktesystem zu verdeutlichen und die Schülerinnen und Schüler dazu aufzufordern eine vorgegebene Mindestmenge an Punkten zu sammeln.
Was sind die Vorteile von Blütenaufgaben?
Alle Schülerinnen und Schüler sollten stets gemäß ihres Lernstandes und ihres Potentials gefördert bzw. gefordert werden. Im Unterricht soll dies durch die sogenannte Binnendifferenzierung ermöglicht werden. Blütenaufgaben können hier einen wertvollen Beitrag leisten, da sie sowohl für leistungsschwache als auch für leistungsstarke Schülerinnen und Schüler geeignet sind. Dies führt zu einer effektiven Nutzung der zur Verfügung stehenden Lernzeit.
Obwohl Blütenaufgaben noch weitere Vorteile besitzen, ist es mir wichtig diesen Aspekt voran zu stellen und zu betonen. Während leistungsschwache Schülerinnen und Schüler im regulären Unterricht häufig an einen Punkt kommen, an dem sie dem Unterricht auf Grund von Überforderung nicht mehr folgen können, fühlen sich Hochbegabte und Hochleister häufig von Langeweile durch Unterforderung geplagt. Dies ist für beide Randgruppen frustrierend. Daher ist es wichtig Möglichkeiten der Binnendifferenzierung auszuloten und Lösungen für alle Schülerinnen und Schüler einer Lerngruppe zu erarbeiten. Aus meiner Sicht können Blütenaufgaben hierzu beitragen.
Die eigenständige Auswahl der zu bearbeitenden Teilaufgabe(n) schult die Selbsteinschätzung der Schülerinnen und Schüler. Die teilweise geöffneten sowie die offenen Aufgaben laden dazu ein individuelle Lösungswege zu finden. Insgesamt fördern Blütenaufgaben das eigenständige und selbstregulierte Lernen.
Passendes Lernmaterial von Kiwole
Das von mir entwickelte Lernmaterial enthält jeweils vier Teilaufgaben je Blütenaufgabe. Ich habe mich dazu entschieden den Schwierigkeitsgrad sowie die Öffnung der Aufgaben nicht konsequent nach unten zu steigern. Stattdessen habe ich eine geringfügige Durchmischung der Aufgaben bevorzugt, wobei am Anfang stets eine leichte Aufgabe zu finden ist, die von allen Schülerinnen und Schülern zu lösen sein sollte. Mir war es wichtig, die Motivation der Lernenden nicht gleich zu Anfang zu zerstören, sondern ein positives Einstiegserlebnis zu ermöglichen.
Eine alternative Form das Material im Unterricht einzusetzen besteht darin die einzelnen Teilaufgaben auszuschneiden, zu laminieren und als separate Kärtchen anzubieten, die von den Schülerinnen und Schülern in der Freiarbeit nach Belieben bearbeitet werden können.
Bislang habe ich Blütenaufgaben zu den drei Themenbereichen „Achsensymmetrie“, „Brüche“ und „Zahlenfolgen“ erstellt. Zu finden sind diese bei Eduki unter folgenden Links:
- Ergänzendes Material zu Achsensymmetrie – Blütenaufgaben
- Brüche und Bruchdarstellung – Blütenaufgaben
- Zahlenfolgen verstehen und fortführen – Blütenaufgaben
Als kleinen Vorgeschmack kannst du dir gerne eines meiner Arbeitsblätter aus der Reihe „Zahlenfolgen“ kostenlos herunterladen und ausdrucken. Tiergreifende Informationen zum Thema Zahlenfolgen findest du in meinem Artikel „Zahlenfolgen verstehen und fortsetzen„.
Anregungen zu weiteren Themenbereichen nehme ich gerne entgegen. Schreib mir einfach eine Mail oder hinterlasse einen Kommentar unter diesem Artikel.
Hast du bereits Erfahrungen mit dem Einsatz von Blütenaufgaben im Unterricht gemacht? Berichte mir gerne davon!
Literatur:
Bruder, R. (2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung – Wege zu einem anspruchsvollen Mathematikunterricht für alle, math-learning [online] https://www.math-learning.com/files/extremal.pdf [abgerufen am 05.03.2024]
Schupp, H. (2003): Thema mit Variationen. Aufgabenvariation im Mathematikunterricht. Hildesheim: Franzbecker
Roth, J., Ames, J. (2014): Beiträge zum Mathematikunterricht 2014 (S. 1047–1050). Münster: WTM-Verlag
abrufbar unter https://eldorado.tu-dortmund.de/bitstream/2003/33335/1/BzMU14-4ES-Salle-432.pdf [abgerufen am 05.03.2024]
