In meinem Blogartikel „Wie viele Würfelnetze gibt es?“ habe ich dich aufgefordert, dir Gedanken über Würfelnetze zu machen. Heute möchte ich dir einige spielerische Aufgaben rund ums Quadernetz vorstellen.
Was ist ein Quadernetz?
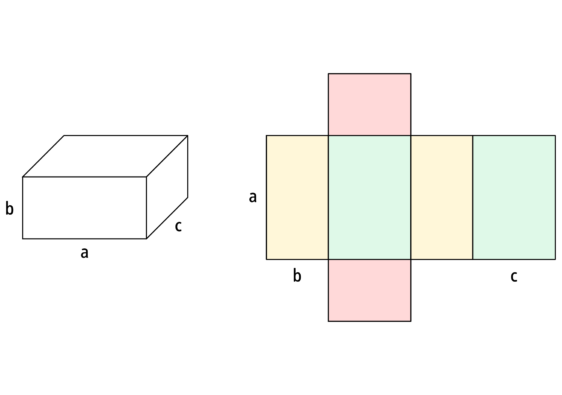
Ein Quader hat sechs rechteckige Flächen, zwölf Kanten und acht Ecken.
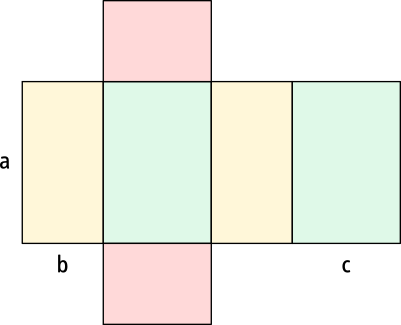
Jeweils zwei seiner Flächen sind gleich groß. Besonders gut ist dies am Quadernetz erkennbar. Denn das Netz des Quaders besteht aus sechs rechteckigen Flächen, wobei jeweils zwei gleich groß sind. Ich habe sie hier zur Veranschaulichung in den gleichen Farben dargestellt. Faltest du dieses zweidimensionale Quadernetz zusammen, so erhältst du den dreidimensionalen Quader.
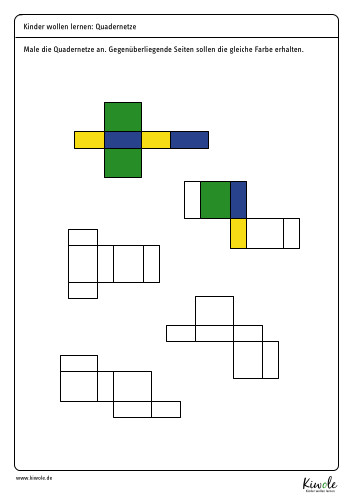
Hierzu habe ich dir ein Arbeitsblatt vorbereitet, auf dem du die Quadernetze so anmalen kannst, dass gegenüberliegende Seiten die gleiche Farbe bekommen.
Welche Kanten stoßen aneinander?
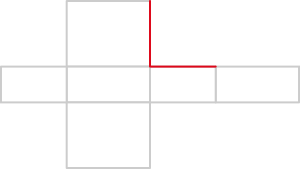
Und hier kommt gleich die nächste Knobelaufgabe: Stell dir vor, du faltest das folgende Quadernetz zu einem Quader zusammen. Welche Kanten würden dabei aneinanderstoßen? Ein Kantenpaar, welches zusammengehört, ist bereits rot markiert.
Das räumliche Vorstellungsvermögen schulen
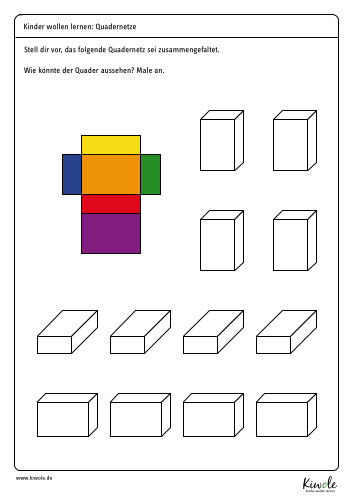
Die oben gezeigten Aufgaben schulen bereits dein räumliches Vorstellungsvermögen. Doch nun gehen wir noch einen Schritt weiter. Stelle dir vor, das farbenfrohe Quadernetz sei zusammengefaltet. Wie könnte der Quader aus den unterschiedlichen Perspektiven aussehen? Auf dem folgenden Arbeitsblatt kannst du es ausprobieren.
Weitere Arbeitsblätter zum Quadernetz
Viele weitere Arbeitsblätter findest du in meiner Materialsammlung „Einführung Quadernetze – inklusive Bastelvorlage Quader“, die sich an Einsteiger richtet. Für Fortgeschrittene empfehle ich „Quadernetze für Fortgeschrittene – inklusive Bastelvorlage“ sowie „Quadernetze zusammensetzen – Rätsel für Fortgeschrittene“. Ich wünsche dir viel Spaß damit!
Weiterführende Aufgaben findest du in meinem Blogartikel „Quaderoberfläche – Die Oberfläche des Quaders berechnen“.
