Manchmal brauchen Kinder kleine Herausforderungen abseits des Lehrplans. Heute stelle ich dir die Dreieckszahlen vor, welche insbesondere für mathematisch interessierte Kinder in der Grundschule sowie der weiterführenden Schule fesselnd sein können.
Was sind Dreieckszahlen?
Von der Eins ausgehend, werden die natürlichen Zahlen addiert. Das Ergebnis sind die Dreieckszahlen:
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
Die ersten Dreieckszahlen lauten also 1, 3, 6 und 10. Doch wie geht die Reihe weiter? Dies könnte die erste Aufgabe für unsere kleinen Knobelfans sein.
Warum heißten die Dreieckszahlen Dreieckszahlen?
Die Dreieckszahlen lassen sich auch grafisch darstellen. Eine beliebte Darstellungsform sind Dreiecke, die sich aus einzelnen Punkten zusammensetzten. So gesehen erklärt sich der Name von selbst.
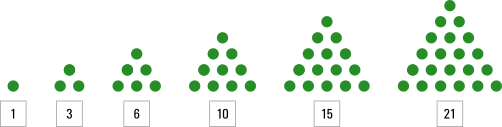
Doch dies ist nicht die einzige mögliche grafische Darstellung. Wenn dein Kind mag, kann es gerne nach weiteren Darstellungen suchen. Ihm fällt bestimmt etwas ein!
Entdecke Muster
Die nächste Knobelaufgabe ist ebenfalls offen gestellt: Gibt es Muster innerhalb der Dreieckszahlen? Fallen dir mathematische Zusammenhänge auf? (Hier eine kleine Anregung: Schaue mal, welche Dreieckszahlen gerade und welche ungerade sind.)
Erinnerst du dich an meinen Blogartikel „Das Pascalsche Dreieck und seine verborgenen Muster„? Wo finden sich die Dreieckszahlen innerhalb des Pascalschen Dreiecks wieder?
Die Dreieckszahlen in unserem Alltag
Die nächste Forscherfrage ist schon etwas komplizierter: Wo finden wir die Dreieckszahlen im Alltag wieder?
Hier ein kleines Beispiel: Stellen wir uns vor, eine Gruppe Freundinnen begrüßt sich üblicherweise mit einer Umarmung. Treffen zwei Freundinnen aufeinander, wird es eine Umarmung geben. Treffen hingegen drei Freundinnen aufeinander, wird es drei Umarmungen geben. Wenn sich vier Freundinnen treffen, kommt es zu sechs Umarmungen. Bei fünf Freundinnen sind es zehn Umarmungen. Die Anzahl der Umarmungen entspricht den Dreieckszahlen.
Die Gaußsche Summenformel
Der Rechenweg 1 + 2 + 3 + 4 + … kann insbesondere bei den größeren Zahlen sehr aufwendig sein. Doch es gibt eine Alternative: die Gaußsche Summenformel. Sie lautet:
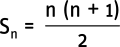
Hierbei ist Sn die Summe der ersten n natürlichen Zahlen und n eine positive ganze Zahl.
Die Gaußsche Summenformel wurde nach dem deutschen Mathematiker Carl Friedrich Gauß benannt. Sie wird auch „kleiner Gauß“ genannt.
Die Forscherfrage hierzu lautet: Vergleiche den rechnerischen Aufwand, indem du beide Rechenwege für unterschiedliche Zahlen ausprobierst. Starte mit kleinen Zahlen wie n = 5 oder n = 7, steigere dich zu n = 10 oder n = 15 und versuche es schließlich mit größeren Zahlen wie n = 35 oder n = 100.
Weiterführendes Material
Nutze die oben aufgeführten Ideen als Ausgangspunkt und stelle für dein Kind individuell auf seinen Wissensstand und seine Anforderungen angepasste Aufgaben zusammen. Dabei darf das Kind auch gerne eigene Fragen zu den Dreieckszahlen äußern und weitere Ideen entwickeln. So wird das Lernen zu einem spannenden, offenen Abenteuer!
Zu den Dreieckszahlen habe ich Arbeitsblätter entwickelt. Du findest sie in meinem Material „Mathe trifft Kunst: Einführung Dreieckszahlen“ auf Eduki. In meinem Shop ist darüber hinaus ein Poster erhältlich.
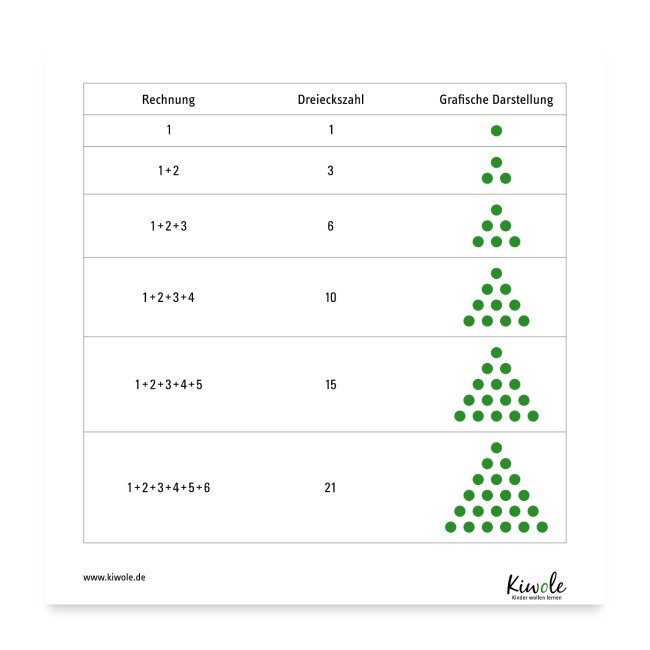
Die Dreieckszahlen zählen zu den figurierten Zahlen, über die ich bereits in meinem Blogartikel „Wachsende Muster – Figurierte Zahlen“ schrieb. Schau doch mal rein für noch mehr neue Lernideen!
Viel Spaß beim Knobeln!
