Kreise lassen sich in Kreissektoren unterteilen, so wie du eine Pizza in einzelne Pizzastücke teilen kannst. Jedes Stück deiner Pizza ist ein Kreissektor. Wir nennen ihn auch „Kreisausschnitt“.
Neben der Pizza lassen sich noch viele weitere Beispiele im Alltag finden. Hier siehst du etwa einen Farbkreis, der in sechs farbige Flächen unterteilt ist. Jede dieser Flächen ist ein Kreissektor.

Der Kreissektor mathematisch beschrieben
Ein Kreissektor ist also eine Teilfläche des Kreises. Er wird durch zwei Radien und einen Kreisbogen begrenzt.
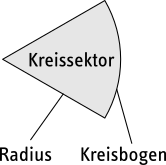
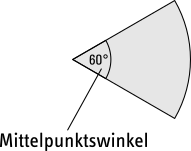
Jeder Kreissektor ist eindeutig bestimmt durch seinen Radius und seinen Mittelpunktswinkel. Im oben dargestellten Farbkreis ist der Mittelpunktswinkel jedes Kreissektors 60° groß.
Einen Kreis in einzelne Sektoren unterteilen
Möchtest du einen Kreis in beliebig viele gleich große Kreissektoren unterteilen, so musst du den Mittelpunktswinkel eines einzelnen Sektors bestimmen. Hierzu teilst du den Vollwinkel von 360° durch die Anzahl der Kreissektoren.
Möchtest du beispielsweise einen Farbkreis mit neun Farbflächen erstellen, so rechnest du 360° : 9 = 40°. Der Mittelpunktswinkel jedes Sektors muss also 40° groß sein.
Praktische Beispiele und Anwendungen
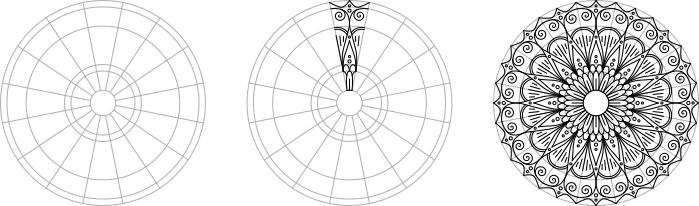
Möchtest du ein Mandala entwerfen, so musst du zunächst einen Kreis in Sektoren unterteilen, um anschließend jeden Sektor mit dem gleichen Muster füllen zu können. Eine detaillierte Anleitung hierzu findest du in meinem Blogartikel „Mandalas selber zeichnen mit Hilfe eines Fineliners“.
Auch beim Zeichnen von regelmäßigen Sternen kann dir die Einteilung des Kreises in einzelne Sektoren nützlich sein. Schau dir dazu das folgende Beispiel an:

Nun bist du dran! Schnapp dir einen angespitzten Bleistift, ein Geodreieck und einen Zirkel und zeichne deine ersten Kreissektoren. Du wirst sehen, dass es gar nicht so kompliziert ist.
Arbeitsblätter zu diesem Thema findest du übrigens bei Eduki in meinem Material „Einführung Kreissektor/Kreisausschnitt“. Ich wünsche dir viel Spaß damit!
(Alle Texte und Bilder sind urheberrechtlich geschützt. Weitere Informationen findest du hier.)