Es gibt viele unterschiedliche Dreiecke. Beispielsweise stumpfwinklige, gleichschenklige und rechtwinklige Dreiecke. Der Basiswinkelsatz bezieht sich nur auf gleichschenklige Dreiecke! Daher solltest du im ersten Schritt in der Lage sein, gleichschenklige Dreiecke sicher von anderen Dreiecken zu unterscheiden.
Was sind gleichschenklige Dreiecke?
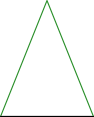
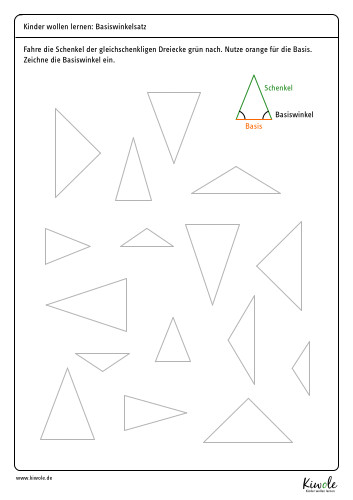
Gleichschenklige Dreiecke haben zwei gleich lange Seiten. In der folgenden Abbildung sind diese Seiten grün markiert. Wir nennen sie die „Schenkel“.
(Möchtest du noch einmal nachlesen, wie du verschiedene Dreiecke voneinander unterscheiden kannst, so empfehle ich dir meinen Blogartikel „Dreiecksarten – Dreiecke auf clevere Art unterscheiden lernen„, der eine gute, leicht verständliche Übersicht enthält.)
Was ist ein Basiswinkel?
In der folgenden Abbildung siehst du, dass diejenige Seite des gleichschenkligen Dreiecks, die nicht zu den beiden gleich langen Seiten gehört, „Basis“ genannt wird. Ich habe sie orange markiert.
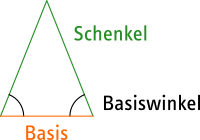
Die Winkel, die an der Basis anliegen, nennen wir Basiswinkel. Vielleicht magst du es dir auch lieber so merken: Die Winkel, die den gleich langen Seiten gegenüber liegen, sind die Basiswinkel.
Diese Begrifflichkeiten sind sehr wichtig. Darum habe ich dir hier ein Arbeitsblatt vorbereitet, auf dem du sie üben kannst. Fahre die Schenkel grün nach. Nutze orange für die Basis und zeichne bei allen Dreiecken die Basiswinkel ein.
Was besagt der Basiswinkelsatz?
Der Basiswinkelsatz besagt, dass in einem gleichschenkligen Dreieck die beiden Winkel gegenüber den gleich langen Seiten gleich groß sind. Das bedeutet: Die Basiswinkel sind gleich groß.
Wozu brauche ich den Basiswinkelsatz?
In der Schule verwendest du den Basiswinkelsatz …
- um unbekannte Winkel in gleichschenkligen Dreiecken zu berechnen
- um zu zeigen, dass ein Dreieck gleichschenklig ist
- um unbekannte Winkel in Drachenvierecken und Rauten, die sich aus zwei gleichschenkligen Dreiecken zusammensetzen, zu berechnen
Weitere Übungen habe ich dir in meinem Material „Einführung gleichschenklige Dreiecke und Basiswinkelsatz“ zusammengestellt, welches du auf eduki findest. Viel Spaß damit!
