Als ich ein Kind war, spielten wir in der Pause häufig Fangen auf dem Schulhof. Manchmal stellte ich mir vor, wie es wohl aussehen würde, wenn man die Wege, welche wir auf dem Schulhof liefen, mit Straßenkreide aufzeichnen würde. Was ich damals nicht wusste: Tatsächlich gibt es in der Mathematik einen Namen für die so entstandenen Kurven. Die Spur des Verfolgers nennt man nämlich Verfolgungskurve.
Die Radiodrome
Hätte man all die Wege aufgezeichnet, die wir damals auf dem Schulhof nahmen, so hätte das Ergebnis vermutlich wie ein riesiges Wollknäuel ausgesehen. Schauen wir uns das Problem deshalb zunächst einmal sehr vereinfacht an. Nehmen wir an, der Verfolgte startet an einem Punkt und läuft von dort aus immer geradeaus. Interessant ist nun die Kurve des Verfolgers. Denn er würde nur dann eine Gerade laufen, wenn er direkt hinter dem Verfolgten stünde. Steht er aber in der Ebene versetzt, so entsteht eine Verfolgungskurve, die Radiodrome genannt wird.
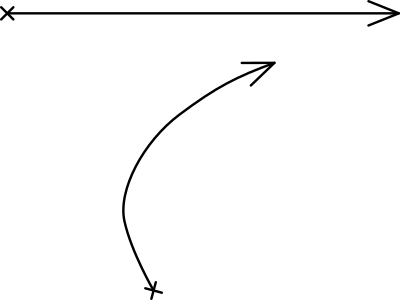
Pierre Bouguer beschrieb diese Kurve 1732 als Erster. Er war unter anderem Professor für Schifffahrtskunde und stellte sich daher keine Kinder vor, die Fangen spielen, sondern ein geradlinig fahrendes Schiff, welches von einem anderen Schiff verfolgt wird. Ebenso kann man sich einen Hund vorstellen, der einen geradlinig laufenden Hasen verfolgt.
Verfolgungskurven mit mehreren Verfolgern
Stellen wir uns jetzt vor, auf dem Schulhof sei ein großes Quadrat aufgemalt. An jeder Ecke des Quadrats steht ein Kind. Das erste Kind verfolgt das zweite Kind, während das zweite Kind das dritte verfolgt. Das dritte Kind wiederum verfolgt das vierte Kind und das vierte Kind verfolgt das erste Kind. So entstehen vier Verfolgungskurven. Unter der Annahme, dass alle Kinder gleich schnell laufen, treffen sie sich am Ende genau in der Mitte.
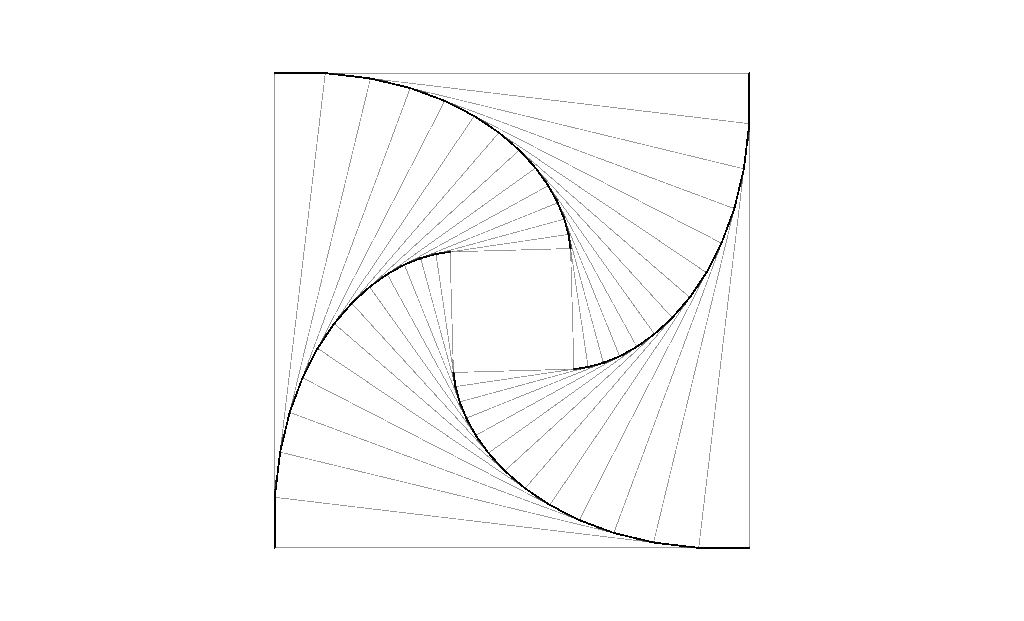
Diese vier Verfolgungskurven lassen sich auch ganz leicht durch Pappquadrate veranschaulichen. Die Anleitung zu diesem kleinen Bastelprojekt findest du in meinem Eduki-Material „Wir basteln eine Op-Art Verfolgungskurve!“. (Kleiner Tipp: Das Material lässt sich auch ganz wunderbar im Kunstunterricht zum Thema „Op-Art“ einsetzen. Weitere Anregungen hierzu findest du in meinem Op-Art-Blogartikel.)


Auf gleiche Art und Weise könnten sich fünf Kinder verfolgen, die auf einem gleichseitigen Fünfeck stehen. Oder sechs Kinder, die auf einem Sechseck stehen. Hierzu findest du auf Eduki mein Material „Op-Art Verfolgungskurven zum Ausmalen“.

Die Verfolgungskurve im realen Leben
Nun könnte man annehmen, die Verfolgungskurven seien bloß unbedeutende Gedankenspielchen irgendwelcher Mathematiker. Ich gebe zu, dass diese Annahme noch wahrscheinlicher erscheint, wenn man sich die mathematischen Gleichungen dieser Kurven anschaut. Doch es gibt tatsächlich eine ganze Reihe an praktischen Anwendungen. Zum Beispiel im Bereich des Motorsports, in der Luftfahrt oder beim Hockey. Für nähere Informationen empfehle ich dir die wikipedia-Seite zu diesem Thema.